时间:2019-12-13 01:42:36
1、选择题 如图所示,质量为2kg的物体沿倾角为30°的固定斜面匀减速上滑了2m距离,物体加速度的大小为8m/s2,(重力加速度g取10m/s2).在此过程中( )
A.物体的重力势能增加了40J
B.物体的机械能减少了12J
C.物体的动能减少了32J
D.斜面克服摩擦力做了12J功
2、选择题 质量为m的滑块沿着高为h,长为L的粗糙斜面恰能匀速下滑,在滑块从斜面顶端匀速下滑到底端的过程中
[? ]
A.重力对滑块所做的功等于mgh
B.滑块克服阻力所做的功等于mgh
C.合外力对滑块所做的功等于mgh
D.合外力对滑块所做的功为零
3、计算题 如图,半径为R的光滑半圆形轨道ABC在竖直平面内,与水平轨道CD相切于C 点,D端有一被锁定的轻质压缩弹簧,弹簧左端连接在固定的挡板上,弹簧右端Q到C点的距离为2R。质量为m的滑块(视为质点)从轨道上的P点由静止滑下,刚好能运动到Q点,并能触发弹簧解除锁定,然后滑块被弹回,且刚好能通过圆轨道的最高点A。已知∠POC=60°,求:
⑴滑块第一次滑至圆形轨道最低点C时对轨道压力;
⑵滑块与水平轨道间的动摩擦因数μ;
⑶弹簧被锁定时具有的弹性势能。
4、计算题 如图,水平匀强电场的电场强度为E,一个带电小球质量为m,轻质的绝缘细线长为L,静止时小球位于A点,细线与竖直方向成30°角, 求: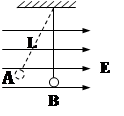
(1)小球带何种电荷?电荷量多少?(5分)
(2)现将小球拉回到竖直方向(图中B点),后由静止释放,小球通过A点位置时的速度大小是多少?(5分)
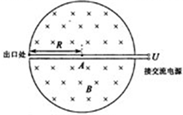
5、简答题 1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的粒子,质量为m、电荷量为+q,在加速器中被加速,加速电压为U.加速过程中不考虑相对论效应和重力作用.
(1)求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比;
(2)求粒子从静止开始加速到出口处所需的时间t;
(3)实际使用中,磁感应强度和加速电场频率都有最大值的限制.若某一加速器磁感应强度和加速电场频率的最大值分别为Bm、fm,试讨论粒子能获得的最大动能Ekm.