时间:2019-12-13 01:41:12
1、计算题 在半径R=5000km的某星球表面,宇航员做了如下实验。实验装置如图甲所示,竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成,将质量m=0.2kg的小球从轨道AB上高H处的某点静止滑下,用力传感器测出小球经过C点时对轨道的压力F,改变H的大小,可测出相应的F大小,F随H的变化关系如图乙所示。求:
(1)圆轨道的半径;
(2)该星球的第一宇宙速度。 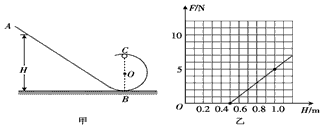
参考答案:解:(1)设该星球表面的重力加速度为g0,圆轨道的半径为r,当H=0.5 m时,有:
mg0(H-2r)=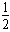 mv02
mv02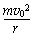 =mg0
=mg0
解得:r=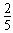 H=0.2 m
H=0.2 m
(2)当H>0.5 m时,有:mg0(H-2r)=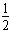 mv2
mv2 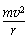 =mg0+F
=mg0+F
即F=g0(2H-1)
由F-H图象可得:g0=5 m/s2
该星球的第一宇宙速度v=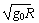 =5 km/s
=5 km/s
本题解析:
本题难度:一般
2、简答题 如图所示,劲度系数为k的轻弹簧,左端连着绝缘介质小球B,右端连在固定板上,放在光滑绝缘的水平面上.整个装置处在场强大小为E、方向水平向右的匀强电场中.现有一质量为m、带电荷量为+q的小球A,从距B球为S处自由释放,并与B球发生碰撞.碰撞中无机械能损失,且A球的电荷量始终不变.已知B球质量为A球质量的3倍,A、B小球均可视为质点.求:
(1)A球与B球碰撞前瞬间的速度v0;
(2)求A球与B球第一次碰撞后瞬间,A球的速度v1和B球的速度v2;
(3)B球被碰后的运动为周期性运动,其运动周期T=2π
 参考答案:(1)设A球与B球碰撞前瞬间的速度为v0, 本题解析: 本题难度:一般 3、填空题 如图所示,在水平向左的匀强电场中,一根不可伸长的绝缘细线长度为L,一端拴一个质量为m电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平伸直的位置A然后将小球由静止释放,小球沿弧线运动到细线与水平方向成θ=60°的位置B时速度为零.则电场强度E=______,小球运动过程中的最大速率为______. 参考答案:由动能定理可知: 本题解析: 本题难度:一般 4、实验题 将质量为1 kg的物体以20 m/s的初速度竖直向上抛出,当物体落回原处时的速度大小变为16 m/s,则在整个过程中,物体克服阻力做的功是__________J. 参考答案:72 本题解析:整个过程只有阻力做功,设为W,根据动能定理有: 本题难度:简单 5、选择题 (附加题)如图所示,一个光滑的四分之一圆弧与一段粗糙水平地面相连,地面右边有一竖直挡板C,它和圆弧底端B的距离为s=9.5m,圆弧的半径R=5m,一小滑块与水平地面之间的动摩擦因数为μ=0.1,现让小滑块从圆弧轨道的顶端A由静止自由滑下,假设小滑块每次与挡板相碰后以原速率返回,重力加速度g取10m/s2,问: 参考答案:(1)vB=10m/s 本题解析: 本题难度:一般 |