时间:2019-07-11 04:19:43
1、选择题 我们的银河系的恒星中大约四分之一是双星。某双星是由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动。由天文观察测得其运动周期为T,S1到C点的距离为r1,S1和S2的距离为r,已知引力常量为G。由此可求出S2的质量为
[? ]
A、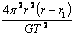
B、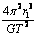
C、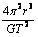
D、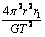
参考答案:D
本题解析:
本题难度:一般
2、选择题 太阳围绕银河系中心的运动可视为匀速圆周运动,其运动速度约为地球绕太阳公转速度的7倍,其轨道半径约为地球绕太阳公转轨道半径的2×109倍,为了粗略估算银河系中恒星的数目,可认为银河系的所有恒星的质量都集中在银河系中心,且银河系中恒星的平均质量约等于太阳的质量,则银河系中恒星的数目约为( ? )
A.1015
B.1013
C.1011
D.109
参考答案:C
本题解析:
本题难度:一般
3、选择题 一行星绕恒星作圆周运动。由天文观测可得,其运动周期为T,速度为v,引力常量为G,则
[? ]
A.恒星的质量为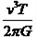 ?
?
B.行星的质量为
C.行星运动的轨道半径为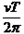 ?
?
D.行星运动的加速度为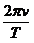
参考答案:ACD
本题解析:
本题难度:一般
4、选择题 “嫦娥二号”是我国月球探测第二期工程的先导星。若测得“嫦娥二号”在月球(可视为密度均匀的球体)表面附近圆形轨道运行的周期T,已知引力常量为G,半径为R的球体体积公式 ,则可估算月球的
,则可估算月球的
[? ]
A.密度?
B.质量?
C.半径?
D.自转周期
参考答案:A
本题解析:
本题难度:一般
5、选择题 一艘宇宙飞船在一颗星球表面附近沿着圆形轨道绕该星球近地飞行,为了要估测该星球的平均密度,则该飞船中宇航员只需要测定的一个参量是
[? ]
A.飞船的环绕半径?
B.行星的质量?
C.飞船的环绕周期?
D.飞船的环绕速度
参考答案:C
本题解析:
本题难度:简单