时间:2019-07-11 04:14:46
1、选择题 两个小球在一条直线上相向运动,若它们相互碰撞后都停下来,则两球碰前 ( )
A.质量一定相等
B.速度大小一定相等
C.总动量一定为零
D.动量一定相同
2、简答题 如图8-3-12所示,一块足够长的木板,放在光滑水平面上,在木板上自左向右放有序号是1、2、3、…、n的木块,所有木块的质量均为m,与木板间的动摩擦因数都相同.开始时,木板静止不动,第1、2、3、…、n号木块的初速度分别是v0、2v0、3v0、…、nv0,方向都向右,木板的质量与所有木块的总质量相等.最终所有木块与木板以共同速度匀速运动.设木块之间均无相互碰撞,木板足够长,试求: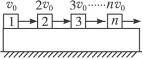
图8-3-12
(1)所有木块与木板一起匀速运动的速度vn;
(2)第1号木块与木板刚好相对静止时的速度v1.
3、实验题 某同学用图甲所示装置通过半径相同的A、B两球的碰撞来寻找不变量,图中PQ是斜槽,QR为水平槽,实验时先使A球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹,重复上述操作10次,得到10个落点痕迹,再把B球放在水平槽上靠近槽末端的地方,让A球仍从位置G由静止开始滚下,和B球碰撞后,A、B球分别在记录纸上留下各自的落点痕迹,重复这种操作10次,图中O是水平槽末端口在记录纸上的垂直投影点,P为未放被碰小球B时A球的平均落点,M为与B球碰后A球的平均落点,N为被碰球B的平均落点,若B球落点痕迹如图乙所示,其中米尺水平放置,且平行于OP,米尺的零点与O点对齐。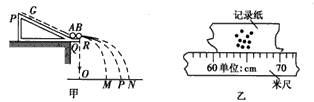
(1)碰撞后B球的水平射程应为____cm。
(2)在以下选项中,哪些是本次实验必须进行的测量?答:____(填选项号)。
A.水平槽上未放B球时,测量A球落点位置到O点的距离
B.A球与B球碰撞后,测量A球落点位置到O点的距离
C.测量A球或B球的直径
D.测量A球和B球的质量
E.测量G点相对于水平槽面的高度
(3)实验中,对入射小球在斜槽上释放点的高低对实验影响的说法中正确的是
[?]
A.释放点越低,小球受阻力越小,入射小球速度越小,误差越小
B.释放点越低,两球碰后水平位移越小,水平位移测量的相对误差越小,两球速度的测量越准确
C.释放点越高,两球相碰时,相互作用的内力越大,碰撞前后动量之差越小,误差越小
D.释放点越高,入射小球对被碰小球的作用越大,轨道对被碰小球的阻力越小
4、计算题 (12分)木板与水平面间的动摩擦因数μ为0.24,木板右端放着质量mB为1.0 kg的小物块B(视为质点),它们均处于静止状态.木板突然受到水平向右的12 N·s的瞬时冲量I作用开始运动,当小物块滑离木板时,木板的动能EKA为8.0 J,小物块的动能EKB为0.50 J,重力加速度取10 m/s2,求: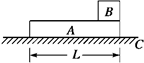
(1)瞬时冲量作用结束时木板的速度v0;?
(2)木板的长度L.?
5、计算题 如图所示,一个质量为m=60 kg的人拽着一个氢气球的软绳,软绳的下端刚好与地面接触,此时人距地面的高度h=60 m,气球与软绳质量M=120 kg,整个系统处于平衡,现此人沿软绳向下滑,问他能否安全回到地面?