时间:2019-07-11 03:50:13
1、实验题 在“用传感器观察电容器的充电和放电”实验中,电路图如图甲。一位同学使用的电源电动势为8.0V,测得放电的I-t图象如图乙所示。(1)若按“四舍五入”法,根据“I-t图线与两坐标轴包围面积”,试计算电容器全部放电过程的放电量为 ;

(2)根据以上数据估算电容器的电容值为 。
参考答案:(1)3.36×10-3C到3.52×10-3C;(2)0.42×10-3F到0.44×10-3F
本题解析:(1)根据四舍五入的原则,图线与坐标轴所围成的面积约为42到44个小格,每个小格表示的电荷量为0.08×10-3C,故电容器的总放电量为3.36×10-3C到3.52×10-3C。
(2)由 得,电容为0.42×10-3F到0.44×10-3F。
得,电容为0.42×10-3F到0.44×10-3F。
考点:电容器的电容及电荷量
本题难度:一般
2、实验题 甲同学设计了如图所示的电路测量电源电动势E及电阻R1和R2的阻值。实验器材有:
待测电源E(不计内阻) 待测电阻R1 待测电阻R2
电压表V(量程为1.5V,内阻很大) 电阻箱R(0~99.99Ω)
单刀单掷开关S1 单刀双掷开关S2 导线若干
(1)先测电阻R1的阻值。请将甲同学的操作补充完整:闭合S1,将S2切换到a,调节电阻箱,读出其示数R和对应的电压表示数U1,保持电阻箱示数不变,________________,读出电压表的示数U2。则电阻R1的表达式为Rl=________________。
(2)甲同学已经测得电阻R1=4.8Ω,继续测量电源电动势E和电阻R2的阻值。该同学的做法是:闭合S1,将S2切换到a,多次调节电阻箱,读出多组电阻箱示数R和对应的电压表示数U,由测得的数据,绘出了如图所示的 图线,则电源电动势E=________________V,,电阻R2=________________Ω。(结果保留小数点后两位)
图线,则电源电动势E=________________V,,电阻R2=________________Ω。(结果保留小数点后两位)
(3)请用笔画线,将实物图连接好。
参考答案:(1)将S2切换到b, ;(2)
;(2) ,
, ;(3)如图所示。
;(3)如图所示。
本题解析:(1)闭合S1,将S2切换到a,电压表测电阻箱的电压;将S2切换到b,电压表测电阻箱和待测电阻R1总的电压,串联电路中 ,故
,故 。
。
(2)闭合S1,将S2切换到a,电压表测电阻箱的电压,由 整理得:
整理得: ,可知图像的截距
,可知图像的截距 ,故电源电动势
,故电源电动势 ;图像的斜率
;图像的斜率 ,故
,故 。
。
(3)实物电路图如右图所示。连接实物图需注意:①尽量保持导线的连接状况与原理图一致;②保证电流从电表的正接线柱流入;③各条连线不能相互交叉。
考点:
本题难度:一般
3、实验题 在“测定金属的电阻率”的实验中,某同学进行了如下操作:
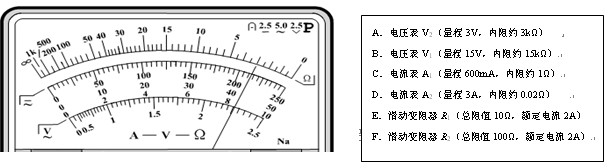
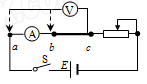
参考答案:(1)3.0;(2)A,C,E;(3)b
本题解析:(1)欧姆表的表盘读数为3.0,乘以倍率(´1挡),阻值R=3.0 .
.
(2)因电源电动势为4v,待测电阻丝上的电压最高约4v,电流最大约1A。为了安全、准确、方便地完成实验,电压表、电流表示数应较大,故应选A、C.滑动变阻器选用总阻值10Ω的E,采用限流电路,就可以有明显的调节电压的作用。
(3)由于待测电阻小,采用电流表外接,电压表的左端应与电路中的b点相连。
考点:测量金属丝的阻值
本题难度:一般
4、实验题 .某同学将铜片和锌片插入水果中制成一个“水果电池”,该同学利用下列所给器材测量水果电池的电动势E和内阻r。
A.电流表G1(内阻Rg=15Ω,满偏电流IA="2" mA)
B.电流表G2(量程10 mA,内阻约2Ω)
C.滑动变阻器R1(0~1000Ω)
D.电阻箱R2(0~9999.9Ω)
E.待测水果电池(电动势E约4 V,内阻,约500Ω)
F.开关S,导线若干
该同学利用以上仪器,测量了多组数据,并记录在下图中的坐标纸上,试根据他所测得的数据,在下面的方框中画出该同学实验的电路图:

(2) 请根据电路图,将下图中的实物连接成实验用的电路。
(3)请你在第(1)题图中把已经描绘出的坐标点连成U—I图线,并根据描绘出的图线可得出水果电池的电动势E= V,内电阻r= Ω.
(4)水果电池的制作非常简易,那么在生活中我们是否可以用水果电池来代替干电池给小电珠供电呢,说明原因: 。
参考答案:
(1): (2)
(3)3.8 470 (每空2分,画图2分,共6分)
(4)不可以,因为水果电池的内阻太大了 (2分)
本题解析:(1)G1 和电阻箱R2串联充当电压表,
(2)略
(3)根据纵坐标可以看出E=3.8v,斜率表示内阻r=2.8/0.0059=470Ω
(4)小电珠电阻太小,水果电源的内阻太大,与水果电池相连小电珠分压太小,根本不会亮。所以不可以。
本题难度:一般
5、实验题 (11分)小华、小刚共同设计了图甲所示的实验电路,电路中的各个器材元件的参数为:电池组(电动势约6V,内阻r约3 )、电流表(量程2.0A,内阻rA=0.8
)、电流表(量程2.0A,内阻rA=0.8 )、电阻箱
)、电阻箱 (0~99.9
(0~99.9 )、滑动变阻器R2(0~Rt)、开关三个及导线若干。他们认为该电路可以用来测电源的电动势、内阻和R2接入电路的阻值。
)、滑动变阻器R2(0~Rt)、开关三个及导线若干。他们认为该电路可以用来测电源的电动势、内阻和R2接入电路的阻值。
(1)小华先利用该电路准确地测出了R2接入电路的阻值。
他的主要操作步骤是:先将滑动变阻器滑片调到某位置,接着闭合S、S2,断开S1,读出电流表的示数I;再闭合S、Sl,断开S2,调节电阻箱的电阻值为3.6 时,电流表的示数也为I.此时滑动变阻器接入电路的阻值为
时,电流表的示数也为I.此时滑动变阻器接入电路的阻值为  .
.
(2)小刚接着利用该电路测出了电源电动势和内电阻。
①他的实验步骤为:
a.在闭合开关前,调节电阻R1或R2至 (选填“最大值”或“最小值”),之后闭合开关S,再闭合 (选填“S1”或“S2”);
b.调节电阻 (选填“R1”或"R2”),得到一系列电阻值 和电流
和电流 的数据;
的数据;
c.断开开关,整理实验仪器。
②图乙是他由实验数据绘出的 图像,图像纵轴截距与电源电动势的乘积代表 ,电源电动势E= V,内阻r=
图像,图像纵轴截距与电源电动势的乘积代表 ,电源电动势E= V,内阻r=  。(计算结果保留两位有效数字)。
。(计算结果保留两位有效数字)。
参考答案:(1)3.6 (2分) ,(2)①最大值(1分),S1(1分),R1(1分);
②电源内阻和电流表的内阻之和(或 )(2分) ,6.0(2分) ,2.8(2分)
)(2分) ,6.0(2分) ,2.8(2分)
本题解析:(1)本小题就是替代法测电阻,电阻箱的读数即是滑动变阻器的电阻,即电阻为 ;
;
(2)①为保护电路,先要把可变电阻调到最大值;因为最后要画出图像,所以必须要知道电阻的阻值,所以要用到电阻箱这个支路,所以接下来要闭合S1,调节电阻R1.
②由闭合电路欧姆定律 ,可得:
,可得: ,所以纵截距表示内阻和电流表的内阻之和与电动势的比值,图像斜率表示电动势的倒数,所以图像纵轴截距与电源电动势的乘积代表电源内阻和电流表的内阻之和,图像斜率为1/6,所以电动势为6V,纵截距为0.6,则内阻和电流表的内阻之和为
,所以纵截距表示内阻和电流表的内阻之和与电动势的比值,图像斜率表示电动势的倒数,所以图像纵轴截距与电源电动势的乘积代表电源内阻和电流表的内阻之和,图像斜率为1/6,所以电动势为6V,纵截距为0.6,则内阻和电流表的内阻之和为 ,所以电源内阻为
,所以电源内阻为 .
.
考点:本题考查了替代法测电阻、测电源电动势和内阻.
本题难度:一般