时间:2019-07-03 00:09:18
1、选择题 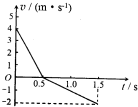 一物块沿斜面直线滑行,初速度方向沿斜面向上,其v-t?图象如图所示,取g=10m/s2.则
一物块沿斜面直线滑行,初速度方向沿斜面向上,其v-t?图象如图所示,取g=10m/s2.则
A.物块下滑的加速度大小为8m/s2
B.物块下滑的加速度大小为2m/s2
C.物块向上滑行的最大距离为2m
D.斜面的倾斜角为30°
参考答案:BD
本题解析:分析:先根据速度时间图象得到物体的运动规律,根据平均速度公式列式求解;然后从速度时间图象分别得到上滑和下滑的加速度,然后受力分析,根据牛顿第二定律列式求解.
解答:A.物体下滑时受到重力、支持力和摩擦力,设此时的加速度为a1
根据牛顿第二定律,有-mgsinθ+f=ma1解得:a1=-2m/s2故B正确A错误;
C.物块向上滑行时做匀加速直线运动,根据平均速度公式,有
即物块向上滑行的最大距离S为1m.故C错误.
D.物体上滑时受到重力、支持力和摩擦力,此时的加速度a2=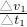 =-8m/s2
=-8m/s2
根据牛顿第二定律,有-mgsinθ-f=ma2?
解得:θ=30°
即斜面的倾角为30°.故D正确.
故选:BD.
点评:本题关键根据速度时间图象得到物体上滑和下滑的加速度,然后受力分析并根据牛顿第二定律列式求解出斜面的倾角.
本题难度:困难
2、选择题 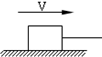 质量为m的物体在水平桌面上被细绳拉着做匀速直线运动,则以下说法中正确的是
质量为m的物体在水平桌面上被细绳拉着做匀速直线运动,则以下说法中正确的是
A.桌面对物体的摩擦力和物体对桌面的摩擦力是一对作用力和反作用力
B.绳对物体的拉力和桌面对物体的摩擦力是一对作用力和反作用力
C.物体所受的重力和桌面所受的压力是一对平衡力
D.绳对物体的拉力和物体对绳的拉力是一对平衡力
参考答案:A
本题解析:分析:作用力与反作用力的关系是大小相等,方向相反,作用在同一条直线上,作用力与反作用力和一对平衡力最大的区别在于作用力与反作用力作用在两个不同的物体上,而一对平衡力是作用在同一个物体上的.
解答:A、桌面对物体的摩擦力和物体对桌面的摩擦力大小相等、方向相反、作用在两个物体上,是一对作用力和反作用力,故A正确;
B、绳对物体的拉力和桌面对物体的摩擦力作用在同一个物体上,不是作用力和反作用力的关系,故B错误;
C、物体所受的重力和桌面所受的压力作用在两个物体上,不是平衡力,故C错误;
D、绳对物体的拉力和物体对绳的拉力是一对作用力和反作用力,故D错误.
故选A
点评:本题主要是考查作用力与反作用力和一对平衡力的区别,作用力与反作用力和一对平衡力最大的区别在于作用力与反作用力作用在两个不同的物体上,而一对平衡力是作用在同一个物体上的.
本题难度:简单
3、选择题 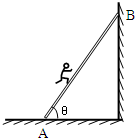 均匀梯子重G1,长为L,一端搁在粗糙地面上,梯子与地面的摩擦系数为μ倾角为θ,另一端搁在光滑墙上.若一重为G2的人沿梯子走上去的过程中梯子不会滑动,则
均匀梯子重G1,长为L,一端搁在粗糙地面上,梯子与地面的摩擦系数为μ倾角为θ,另一端搁在光滑墙上.若一重为G2的人沿梯子走上去的过程中梯子不会滑动,则
A.墙对梯子的作用力减小
B.墙对梯子的作用力增大
C.地对梯子的摩擦力增大
D.地对梯子的弹力不变
参考答案:BCD
本题解析:分析:以A为支点,分析除A点以外人和梯子整体的受力情况,根据力矩平衡条件墙对梯子的作用力.对整体进行受力分析,由共点力平衡条件分析地面对梯子施加的弹力和摩擦力.
解答:
A、B设梯子的长度为L,人离地面的高度为h,设F为墙面对梯子上端B施加的力,则根据力矩平衡得:
FLsinθ=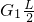 cosθ+G2hcotα,人向上运动,h增大,其他量不变,可见F也随着增大.故A错误,B正确.
cosθ+G2hcotα,人向上运动,h增大,其他量不变,可见F也随着增大.故A错误,B正确.
C、D对人和梯子整体研究,水平方向受到墙的作用力F和地面的静摩擦力f,竖直方向受到总重力G1+G2和地面的支持力N,则由平衡条件可知,N=G1+G2,f=F,所以N保持不变,f增大.故C、D正确.
故选BCD
点评:本题是力矩平衡和共点力平衡的综合应用,要善于确定研究对象,选择解题规律,通过练习培养自己的解题能力.
本题难度:困难
4、选择题 如图所示,物体A静止在斜面体B上,斜面体放在水平面上静止.则物体A受力的情况为
A.重力 弹力 摩擦力
B.下滑力 弹力 摩擦力
C.重力 弹力 摩擦力 下滑力
D.重力 对斜面的压力 摩擦力
参考答案:A
本题解析:分析:物体静止在斜面上,受到重力、斜面的支持力和摩擦力作用.
解答:物体静止在斜面上,由于重力作用物体压紧斜面,斜面对物体有支持力.又由于重力的作用,物体有下滑的趋势,受到斜面的静摩擦力,则物体受到重力、斜面的支持力和摩擦力作用.故A正确,B、C、D错误.
故选A.
点评:本题是基本的受力分析问题.对于受力分析一般按重力、弹力和摩擦力顺序分析.注意下滑力不是物体受到的力.
本题难度:困难
5、选择题 已知合力的大小和方向求两个分力时,下列说法中错误的是
A.若已知两个分力的方向,分解是唯一的
B.若已知一个分力的大小和方向,分解是唯一的
C.若已知一个分力的大小及另一个分力的方向,分解是唯一的
D.此合力可以分解成两个与合力等大的分力
参考答案:C
本题解析:本题可利用解三角形的知识讨论,其中C项是错误的.
本题难度:简单