时间:2019-07-02 23:57:11
1、选择题 质量为m的小球A在光滑的水平面上以速度v与静止在光滑水平面上的质量为2m的小球B发生正碰,碰撞后,A球的动能变为原来的1/9,那么碰撞后B球的速度夫小可能是
A．
B．
C．
D．
参考答案：AB
本题解析：分析：碰后A球的动能恰好变为原来的
，速度大小变为原来的
，但速度方向可能跟原来相同，也可能相反，再根据碰撞过程中动量守恒即可解题．
解答：解：根据碰后A球的动能恰好变为原来的，得：
mv2=?mv02
v=±，碰撞过程中AB动量守恒，则mv0=mv+2mvB
解得：vB=或vB=
故选AB．
点评：本题考查的是动量定律得直接应用，注意动能是标量，速度是矢量，难度适中，属于中档题．
本题难度：简单
2、选择题 如图所示，质量不同的木块A．B用轻弹簧连接静止于光滑水平面上，开始两木块间的距离为L，现将两木块拉开到相距1.5L时由静止释放，关于释放以后的运动情况有以下说法中正确的是（ ）
A．两木块相距最近时可达0.5L
B．两木块相距又为L时，两木块的动量相同
C．两木块一定能同时各自回到刚释放时的位置
D．两木块不可能同时各自回到刚释放时位置
参考答案：A、开始两木块间的距离为L，现将两木块拉开到相距1.5L时由静止释放，弹簧形变量是0.5L，
两木块相距最近时木块速度为零，根据能量守恒，两木块相距最近时弹簧的弹性势能等于相距1.5L时的弹簧的弹性势能，
所以两木块相距最近时弹簧形变量是0.5L，即最近时可达0.5L．故A正确
B、质量不同的木块A．B用轻弹簧连接静止于光滑水平面上，系统动量守恒，系统初动量为零，所以两木块相距又为L时，两木块的动量大小相等，方向相反，动量是矢量．故B错误
C、根据能量守恒得两木块一定能同时各自回到刚释放时的位置，故C正确，D错误．
故选AC
本题解析：
本题难度：一般
3、填空题 静止在水面上的船长为L、质量为M，一个质量为m的人站在船头，当此人由船头走到
船尾时，不计水的阻力，人对河岸的位移大小是?
参考答案：ML/（M＋m）
本题解析：略
本题难度：简单
4、简答题 A的轻绳悬于足够高的天花板上.现让球B自弹簧自然长度处由静止释放后，在竖直方向做振幅为x0的简谐运动.当球B运动至最低点时剪断轻绳，经过时间t，A、B两球的加速度相同，球A的速度为va.重力加速度为g.求：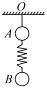
图10
（1）此时球B的速度；
（2）球A下落的距离.
参考答案：（1）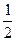
(3gt-vA)? (2)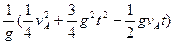
本题解析：（1）设在时间t内，弹簧弹力对A的冲量为I，则
对A球，有mgt+I=mvA?①
对B球，有2mgt-I=2mvB?②
联立得3mgt=mvA+2mvB
解得vB=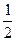?(3gt-vA)?③
(2)设B球做简谐运动至最低点时，弹簧的弹性势能为Ep，由机械能守恒,有2mg·2x0=Ep?④
剪断细线后的下落过程中，A、B及弹簧组成系统的机械能守恒，则有
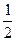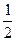mgh+2mg(h-2x0)+Ep=mv2A+·2mv2B?⑤
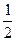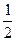由④⑤式得3mgh=mv2A+·2mv2B
解得h=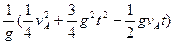?⑥
本题难度：简单
5、填空题 甲、乙两个溜冰者，质量分别为m甲=59kg、m乙=50kg，均以6.0m/s速度在同一条直线上相向滑行，甲手持一个质量为1.0kg的球，他将球抛给乙，乙再把球抛还甲，这样抛接若干次后，当甲接到球后的速度恰好为零时，乙的速度大小是?m/s，方向与乙原来滑行方向?。
参考答案：1.2，相反
本题解析：根据题意，在整个过程中，系统动量守恒，则（m甲+m球）v1+m乙v2=m乙v3
解得v3=1.2m/s,根据动量守恒定律可以判断方向为与乙原来滑行方向相反。
点评：本题考查了对系统动量守恒定律的利用。在运用之前应该先判断是否满足动量守恒的前提条件。
本题难度：简单