时间:2019-07-02 23:45:26
1、选择题 如图所示，半径为及、圆心角为600的光滑圆弧槽，固定在高为h的平台上，小物块从圆?弧槽的最高点A静止开始滑下，滑出槽口?B时速度水平向左，小物块落在地面上C点，B、C两点在以O2点为圆心的圆弧上，02在B点正下方地面上，则?（ ）
A．4R=h
B．2R=h
C．R=h
D．R=2h
参考答案：根据动能定理得，mgR（1-cos60°）=12mvB2，解得vB=
本题解析：
本题难度：一般
2、简答题 如图所示，行车通过长L=5m的吊索，吊着质量m=1.0×103kg的钢材，以v=2m/s速度沿水平方向匀速行驶，行车突然停车．（g取10m/s2）求：
（1）行车在行驶过程中，吊钩受到的拉力F；
（2）行车突然停车的瞬间，吊钩受到的拉力F′．
参考答案：（1）由二力平衡条件知：F=mg=104N
即行车在行驶过程中，吊钩受到的拉力F等于104N．
（2）由题意知，行车突然停车的瞬间，钢材开始做圆周运动，其所受合力提供向心力，
即：F′-mg=mv2L
∴F′=m（g+v2L）=1.08×104N
即行车突然停车的瞬间，吊钩受到的拉力F′为1.08×104N．
本题解析：
本题难度：一般
3、选择题 一质量为m的小球A用轻绳系于O点，如果给小球一个初速度使其在竖直平面内做圆周
运动，某时刻小球A运动到圆轨道的水平直径的右端点时，如图所示位置，其加速度大小为g，则它运动到最低点时，绳对球的拉力大小为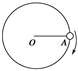
[? ]
A．(3＋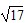
)m
g?
B．7mg
C．(2＋
)mg?
D．6mg
参考答案：B
本题解析：
本题难度：简单
4、选择题 上海磁悬浮线路需要转弯的地方有三处，其中设计的最大转弯处半径达到8000米，用肉眼看几乎是一条直线，而转弯处最小半径也达到1300米．一个质量50kg的乘客坐在以360km/h不变速率驶过半径2500米弯道的车厢内，下列说法正确的是（ ）
A．乘客受到来自车厢的力大小约为200N
B．乘客受到来自车厢的力大小约为539N
C．弯道半径设计特别长可以使乘客在转弯时更舒适
D．弯道半径设计特别长可以减小转弯时列车的倾斜程度
参考答案：对人进行受力分析，如图所示：
根据圆周运动向心力公式得：
F向=mv2R=50×(100)22500N=200N
FN=
本题解析：
本题难度：简单
5、选择题 如图所示，用一连接体一端与一小球相连，绕过O点的水平轴在竖直平面内做圆周运动，设轨道半径为r，图中P、Q两点分别表示小球轨道的最高点和最低点，则以下说法正确的是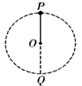
[? ]
A．若连接体是轻质细绳时，小球到达P点的速度可以为零
B．若连接体是轻质细杆时，小球到达P点的速度一定不能为零
C．若连接体是轻质细绳时，小球在P点受到细绳的拉力一定为零
D．若连接体是轻质细杆时，若小球在P点受到细杆的作用力为拉力，在Q点受到细杆的作用力也为拉力
参考答案：D
本题解析：
本题难度：简单