时间:2019-06-29 05:03:14
1、计算题 如图所示,在一底边长为2a,θ=30°的等腰三角形区域内(D为底边中点),有垂直于纸面向外的匀强磁场。现有一质量为m,电荷量为q的带正电的粒子从静止开始经过电势差为U的电场加速后,从D点垂直于EF进入磁场,不计重力与空气阻力的影响。
(1)若粒子恰好垂直于EC边射出磁场,求磁场的磁感应强度B为多少?
(2)改变磁感应强度的大小,粒子进入磁场偏转后能打到ED板,求粒子从进入磁场到第一次打到ED板的最长时间是多少? 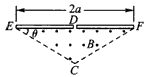
参考答案:解:(1)依题意,设粒子经电场加速射入磁场时的速度为v
由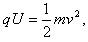 得
得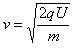 ?①
?①
粒子在磁场中做匀速圆周运动,其圆心在E点,如图(a)所示,半径r1=a ② 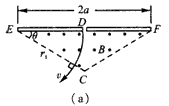
由洛伦兹力提供向心力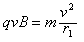 ?③
?③
由①②③式得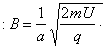
(2)粒子速率恒定,从进入磁场到第一次打到ED板的轨迹与EC边相切时,路程最长,运动时间最长,如图(b)所示,设轨迹半径为r2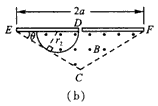
由图中几何关系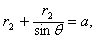 得
得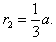
最长时间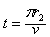
由以上各式联立得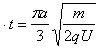
本题解析:
本题难度:困难
2、选择题 两个质量相同、所带电荷量相等的带电粒子a、b,以不同的速率对准圆心O沿着AO方向射入圆形匀强磁场区域,其运动轨迹如图.若不计粒子的重力,则下列说法正确的是( )
A.a粒子带正电,b粒子带负电
B.a粒子在磁场中所受洛伦兹力较大
C.b粒子动能较大
D.b粒子在磁场中运动时间较长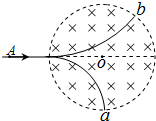
参考答案:粒子向右运动,根据左手定则,b向上偏转,应当带正电;a向下偏转,应当带负电,故A错误.
洛伦兹力提供向心力,即:qvB=mv2r,得:r=mvqB,故半径较大的b粒子速度大,动能也大.故C正确.
由公式;f=qvB,故速度大的b受洛伦兹力较大.故B错误.
磁场中偏转角大的运动的时间也长;a粒子的偏转角大,因此运动的时间就长.故D错误.
故选:C
本题解析:
本题难度:简单
3、计算题 如图(a)所示,在以直角坐标系xOy的坐标原点O为圆心、半径为r的圆形区域内,存在磁感应强度大小为B、方向垂直xOy所在平面的匀强磁场。一带电粒子由磁场边界与x轴的交点A处,以速度v0沿x轴负方向射入磁场,粒子恰好能从磁场边界与y轴的交点C处,沿y轴正方向飞出磁场,不计带电粒子所受重力。
(1)求粒子的荷质比q/m;
(2)若磁场的方向和所在空间的范围不变,而磁感应强度的大小变为B",该粒子仍从A处以相同的速度射入磁场,粒子飞出磁场时速度的方向相对于入射方向改变了θ角,如图(b)所示,求磁感应强度B"的大小。 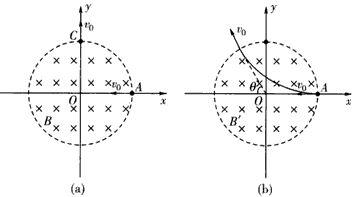
参考答案:解:(1)由几何关系可知,粒子的运动轨迹如图,其半径R=r,洛伦兹力等于向心力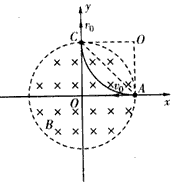
即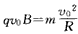
得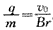
(2)粒子的运动轨迹如图,设其半径为R",洛伦兹力提供向心力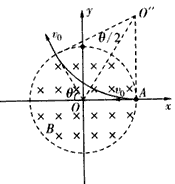
即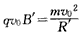
又因为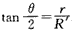
解得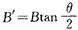
本题解析:
本题难度:困难
4、选择题 质量为m带电量为e的电子以一定速度射入一圆形区域方向垂直于纸面向外的匀强磁场B,速度方向垂直于磁场指向圆心O,离开磁场时速度方向与入射方向成120°角如图所示,那么电子的入射点及在磁场中运动的时间为( )
A.入射点为M点,时间为t=
| πm eB |
| πm 2eB |
| πm 3eB |
| 2πm 3eB |

参考答案:由圆的性质可知,粒子的圆心只能在左下方;故在M、N点的受到的洛仑兹力应指向下方,则由左手定则可得出粒子应由N点入射;
如图所示,由几何关系可知圆心角为60°,故运动时间t=60°360°T=πm3eB.
故选C.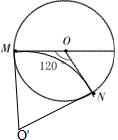
本题解析:
本题难度:简单
5、选择题 如图所示,一束电子以大小不同的速率从同一位置沿图示方向飞入横截面为一正方形的匀强磁场区,在从ab边离开磁场的电子中,下列判断正确的是 
[? ]
A.从b点离开的电子速度最大
B.从b点离开的电子在磁场中运动时间最长
C.从b点离开的电子速度偏转角最大
D.在磁场中运动时间相同的电子,其轨迹一定重合
参考答案:AD
本题解析:
本题难度:一般