时间:2019-06-28 05:21:48
1、选择题 如图所示,木块A的右侧为光滑曲面,曲面下端极薄,其质量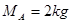 ,原来静止在光滑的水平面上,质量
,原来静止在光滑的水平面上,质量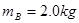 的小球B以v=2m/s的速度从右向左做匀速直线运动中与木块A发生相互作用,则B球沿木块A的曲面向上运动中可上升的最大高度(设B球不能飞出去)是( )
的小球B以v=2m/s的速度从右向左做匀速直线运动中与木块A发生相互作用,则B球沿木块A的曲面向上运动中可上升的最大高度(设B球不能飞出去)是( )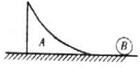
A.0.40m
B.0.20m
C.0.10m
D.0.5m
2、选择题 如图所示,竖直放置的光滑圆轨道被固定在水平地面上,半径r=0.4m,在最低点处有一小球(其半径远小于轨道半径r)。现给小球以水平向右的初速度v0,g取10m/s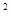 ,如果要使小球运动过程中不脱离圆轨道运动, v0的大小满足的条件可表示为(?)
,如果要使小球运动过程中不脱离圆轨道运动, v0的大小满足的条件可表示为(?)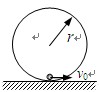
A.v0≥0
B.v0≥4m/s
C.v0≥2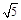 m/s
m/s
D.v0≤2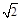 m/s
m/s
3、选择题 一辆小车静止在光滑的水平面上,小车立柱上固定一条长为L、系有小球的水平细绳,小球由静止释放,如图所示,不计一切摩擦,下列说法正确的是:( )
A.小球的机械能守恒,动量不守恒
B.小球的机械能不守恒,动量也不守恒
C.球、车系统的机械能守恒,动量守恒
D.球、车系统的机械能、动量都不守恒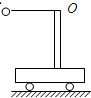
4、选择题 质量为m的小球,从桌面上竖直抛出,桌面离地面高为h,小球能达到的最大高度离地面为H。若以桌面作为重力势能的参考面,不计空气阻力,则小球落地时的机械能为
[? ]
A.mgH
B.mgh
C.mg(H+h)
D.mg(H-h)
5、简答题 如图所示,光滑弧形轨道下端与水平传送带吻接,轨道上的A点到传送带的竖直距离和传送带到地面的距离均为h=5m,把一物体放在A点由静止释放,若传送带不动,物体滑上传送带后,从右端B水平飞离,落在地面上的P点,B、P的水平距离OP为x=2m;若传送带顺时针方向转动,传送带速度大小为v=5m/s,则物体落在何处?这两次传送带对物体所做的功之比为多大?