时间:2019-06-26 05:17:41
1、计算题 （20分）如图所示，水平传送带AB的右端与在竖直面内的用内径光滑的钢管弯成的“9”形固定轨道相接，钢管内径很小.传送带的运行速度v0=4.0m/s，将质量m=1kg的可看做质点的滑块无初速地放在传送带的A端.已知传送带长度L= 4.0 m，离地高度h=0.4 m，“9”字全髙H= 0.6 m，“9”字上半部分圆弧半径R="0.1" m，滑块与传送带间的动摩擦因数μ=0.2，重力加速度g=10 m/s2，试求：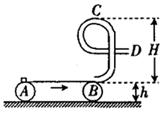
(1)滑块从传送带A端运动到B端所需要的时间；
(2)滑块滑到轨道最高点C时对轨道作用力；
(3)滑块从D点抛出后的水平射程。
2、选择题 如图所示，倾角为30?的光滑轩上套有一个小球和两根轻质弹簧，两弹簧的一端与小球相连，另一端分别用销钉M、N固定于杆上，小球处于静止状态，设拔去销钉M瞬间，小球的加速度大小为6m/s2，若不拔去销钉M，而拔去销钉N瞬间，小球加速度可能是（g=10m/s2）（
A．11m/s2，沿轩向上
B．11m/s2?，沿轩向下
C．1m/s2，沿轩向上
D．1m/s2，沿杆向下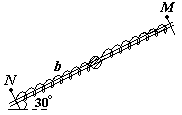
3、选择题 如图所示，一物块以初速度v0滑上正沿逆时针转动的水平传送带，传送带上A、B两点间的距离L=9m．已知传送带的速度v=2m/s，物块与传送带间的动摩擦因数μ=0.2，重力加速度g取10m/s2．下列说法中正确的是（ ）
A．要使物块被传送到B点，初速度应为v0=6m/s
B．要使物块被传送到B点，初速度应为v0=2m/s
C．当物块的初速度v0=4m/s时，物块将以2m/s的速度离开传送带
D．当物块的初速度v0=2m/s时，物块在传送带上先做减速运动，再做加速运动，而后匀速运动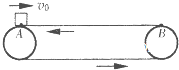
4、计算题 “翻滚过山车”的物理原理可以用如图
所示装置演示，光滑斜槽轨道AD与半径为R＝0.1m的竖直圆轨道(圆心为O)相连，AD与圆O相切于D点，B为轨道的最低点，∠DOB＝37°.质量为m＝0.1kg的小球从距D点L＝1.3m处由静止开始下滑，然后冲上光滑的圆形轨道(g＝10m/s2，sin37°＝0.6，cos37°＝0.8)．求：
(1)小球在光滑斜槽轨道上运动的加速度的大小；
(2)小球通过B点时对轨道的压力的大小；
(3)试分析小球能否通过竖直圆轨道的最高点C，并说明理由．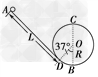
5、填空题 光滑水平面上有A、B两带电小球，A的质量为B的质量的2倍，将两球由静止释放．开始时A的加速度为a，经一段时间后，B的加速度也为a，速度大小为v，则此时，A球的加速度为______，速度大小为______．