时间:2019-06-26 04:45:41
1、计算题 扭摆器是同步辐射装置中的插入件,能使粒子的运动轨迹发生扭摆。其简化模型如图:I、Ⅱ两处的条形 匀强磁场区边界竖直,相距为L,磁场方向相反且垂直于纸面。一质量为m、电量为-q、重力不计的粒子,从靠近平行板电容器MN板处由静止释放,极板间电压为U,粒子经电场加速后平行于纸面射入I区,射入时速度与水平方向夹角θ=30°。
(1)当I区宽度L1=L、磁感应强度大小B1=B0时,粒子从I区右边界射出时速度与水平方向夹角也为30°,求B0及粒子在I区运动的时间t。
(2)若Ⅱ区宽度L2=L1=L、磁感应强度大小B2=B1=B0,求粒子在I区的最高点与Ⅱ区的最低点之间的高度差h。
(3)若L2=L1=L、B1=B0,为使粒子能返回I区,求B2应满足的条件。
(4)若B1≠B2、L1≠L2,且已保证了粒子能从Ⅱ区右边界射入。为使粒子从Ⅱ区右边界射出的方向与从I区左 边界射出的方向总相同,求B1、B2、L1、L2之间应满足的关系式。 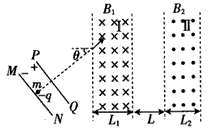
参考答案:解:(1)如图甲所示,设粒子射入磁场I区的速度为v,在磁场I区中做圆周运动的半径为R1,由动能定理和牛顿第二定律得: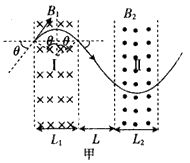 ?
?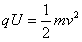 ,
,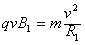
由几何知识得:L=2R1sinθ
联立解得: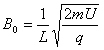
设粒子在磁场I区中做圆周运动的周期为T,运动的时间为t,则: 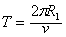 ,
,
联立解得: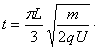
(2)设粒子在磁场Ⅱ区做圆周运动的半径为R2,由牛顿第二定律得: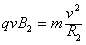
由几何知识可得:h=(R1+R2)(1-cosθ)+Ltanθ
联立解得:
(3)如图乙所示,为使粒子能再次回到I区,应满足R2(1+sinθ)<L[或R2(1+sinθ)≤L] 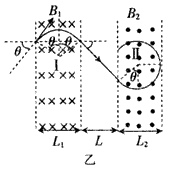
解得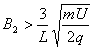 (或B2≥
(或B2≥
(4)如图丙(或图丁)所示,设粒子射出磁场I区时速度与水平方向的夹角为α,由几何知识可得: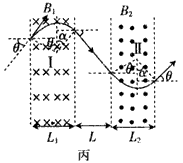 ?
? 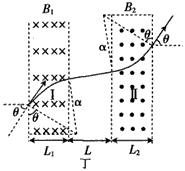
L1=R1(sinθ+sinα)[或L1=R1(sinθ-sinα)]
L2=R2(sinθ+sinα)[或L2=R2(sinθ-sinα)]
解得:B1R1=B2R2
联立解得:B1L1=B2L2
本题解析:
本题难度:困难
2、计算题 (20分)如图所示,半径R = 0.8m的四分之一光滑圆弧轨道位于竖直平面内,与长CD = 2.0m的绝缘水平面平滑连接。水平面右侧空间存在互相垂直的匀强电场和匀强磁场,电场强度E = 40N/C,方向竖直向上,磁场的磁感应强度B = 1.0T,方向垂直纸面向外。两个质量均为m = 2.0×10-6kg的小球a和b,a球不带电,b球带q = 1.0×10-6C的正电,并静止于水平面右边缘处。将a球从圆弧轨道顶端由静止释放,运动到D点与b球发生正碰,碰撞时间极短,碰后两球粘合在一起飞入复合场中,最后落在地面上的P点。已知小球a在水平面上运动时所受的摩擦阻力 f = 0.1mg, PN =
f = 0.1mg, PN =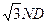 ,取g =10m/s2。a、b均可作为质点。(结果保留三位有效数字)求:
,取g =10m/s2。a、b均可作为质点。(结果保留三位有效数字)求:
(1)小球a与b相碰后瞬间速度的大小v
(2)水平面离地面的高度h
(3)从小球a开始释放到落地前瞬间的整个运动过程中,ab系统损失的机械能ΔE。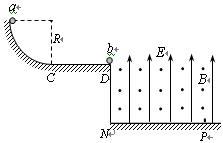
参考答案:(1)v = 1.73m/s
(2)3.46m
(3)1.49×10-4J
本题解析:
(1)设a球到D点时的速度为vD,从释放至D点,
根据动能定理: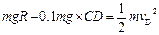 ?(3分)
?(3分)
对a、b球,根据动量守恒定律? mvD =" 2mv?" (2分)
解得:v = 1.73m/s?(2分)
(2)两球进入复合场后,由计算可知Eq = 2mg,两球在洛仑兹力作用下做匀速圆周运动轨迹示意图如右图所示?(1分)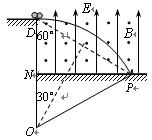
洛仑兹力提供向心力 ?(2分)
?(2分)
由图可知: r = 2h ?(2来源:91考试网 91exam.org分)?解得:h = 2 =3.46m ?(2分)
=3.46m ?(2分)
(3)ab系统损失的机械能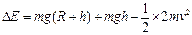 ?(4分)
?(4分)
或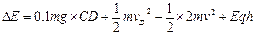 ?解得?
?解得? ?= 1.49×10-4J?(2分)
?= 1.49×10-4J?(2分)
本题难度:一般
3、计算题 如图所示,在x轴上方有垂直于xy平面向里的匀强磁场,磁感应强度为B;在x轴下方有沿y轴负方向的匀强电场,场强为E。一质量为m,电荷量为-q的粒子从坐标原点O沿着y轴正方向射出。射出之后,第三次到达x轴时,它与点O的距离为L。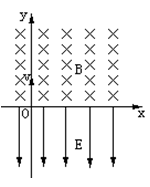
小题1:带电粒子在磁场中做何种运动?
小题2:带电粒子在电场中做何种运动?
小题3:求此粒子射出时的速度v?
小题4:运动的总路程s(重力不计)。
参考答案:
小题1:匀速圆周运动(半周)
小题2:往复运动,匀减速到零后匀加速返回
小题3:运动轨迹如右图L=4R
设粒子初速度为v,qvB=mv2/R
小题4:πL/2+qB2L2/(16mE)
本题解析:分析:粒子在磁场中做圆周运动,转动半周后到达电场先减速再反向加速,以大小不变的速度反向进入磁场,再次偏转;由题意可知半径大小,由洛仑兹力充当向心力可求得粒子的速度;粒子的总路程包括电场中的路程和磁场中的路程,求出两场中的过程即可求出总路程.
解答:解:由题意知第3次经过x轴的运动如图所示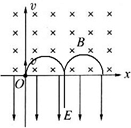
由几何关系:L=4R,设粒子初速度为v,则有:qvB=m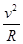 ,可得:v=
,可得:v=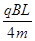 ;?
;?
设粒子进入电场作减速运动的最大路程为L′,加速度为a,则有:v2=2aL′
qE=ma,则电场中的路程:L′=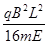
粒子运动的总路程:s=2πR+2L’=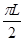 +
+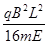
答:粒子在磁场中做匀速圆周运动,在电场中做往复运动,匀减速到零后匀加速返回,粒子射出的速度为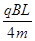 ,粒子的总路程为
,粒子的总路程为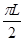 +
+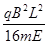 .
.
点评:带电粒子在磁场中的题目关键在于明确圆心和半径,注意要根据题意找出合理的运动过程,从而得出正确的结论.
本题难度:一般
4、计算题 (16分)如图所示,矩形区域MNPQ内有水平向右的匀强电场,虚线框外为真空区域;半径为R、内壁光滑、内径很小的绝缘半圆管ADB固定在竖直平面内,直径AB垂直于水平虚线MN,圆心O恰在MN的中点,半圆管的一半处于电场中。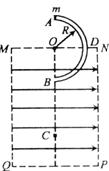
一质量为m,可视为质点的带正电小球从半圆管的A点由静止开始滑入管内,小球从B点穿出后,能够通过B点正下方的C点。重力加速度为g,小球在C点处的加速度大小为5g/3。求:
(1)小球所受电场力的大小;
(2)小球在B点时,对半圆轨道的压力大小;
(3)虚线框MNPQ的宽度和高度满足的条件。
参考答案:(16分)(1)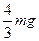 (2)
(2)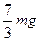 ?(3)
?(3) ,
,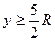
本题解析:略
本题难度:简单
5、简答题 在图中,两平行金属板间有正交的匀强电场和匀强磁场,其中磁场方向垂直板面向里.一个带电油滴从静止由平行板的负极出发,作曲线运动,其轨迹在A点的切线恰为水平,油滴通过A点时吸附了一质量与它相等的静止的不带电的液滴后,一起沿过A点的切线方向作匀速直线运动,重力不计,已知油滴的质量m=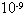 kg,所带电量大小为q=
kg,所带电量大小为q=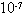 C,电场强度E=100V/m,磁场的磁感强度B=4T,求A点离负极板的距离为多少?
C,电场强度E=100V/m,磁场的磁感强度B=4T,求A点离负极板的距离为多少?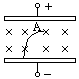
参考答案:0.125m
本题解析: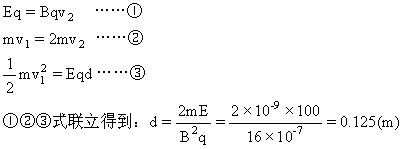
本题难度:一般