时间:2019-06-26 04:00:28
1、简答题 汽车以10m/s的速度通过一座拱桥的最高点,拱桥半径20m,求此车里的一名质量为20kg的小孩对座椅的压力.(g=10m/s2)
2、计算题 如图所示的圆锥摆,绳长为l,绳子一端固定,另一端系一质量为m的质点,在水平面内绕O点作匀速圆周运动,绳子与铅直线的夹角为θ。在质点旋转的过程中,试求:
(1)质点做匀速圆周运动的向心力大小;
(2)质点做匀速圆周运动的周期。 
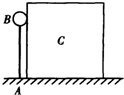
3、简答题 如图所示,长度为L的轻杆上端连着一质量为m的体积可忽略的小重物B.杆的下端用铰链固接于水平面上的A点.同时,置于同一水平面上的立方体C恰与B接触,立方体C的质量为M.今做微小的扰动,使杆向右倾倒,设B与C、C与水平面间均无摩擦,而B与C刚脱离接触的瞬间,杆与地面夹角恰好为
| π 6 |
| m M |
4、选择题 有一个惊险的杂技节目叫“飞车走壁”,杂技演员骑摩托车先在如图所示的大型圆筒底部作速度较小、半径较小的圆周运动,通过逐步加速,圆周运动的半径逐步增大,最后能以较大的速度在竖直的壁上作匀速圆周运动,这时使车子和人整体作匀速圆周运动的向心力是( )
A.圆筒壁对车的静摩擦力
B.筒壁对车的弹力
C.摩托车本身的动力
D.重力和摩擦力的合力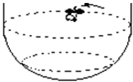
5、简答题 某平面上有一半径为R的圆形区域,区域内、外均有垂直于该平面的匀强磁场,圆外磁场范围足够大,已知两部分磁场方向相反,方向如图所示,磁感应强度都为B,现在圆形区域的边界上的A点有一个电量为q,质量为m的带正离子沿半径方向射入圆内磁场.求:
(1)若离子的速度大小为v1,求该离子在磁场中的轨道半径r;
(2)若离子与圆心O的连线旋转一周时,离子也恰好回到A点,试求该离子的运动速度v;
(3)在离子恰能回到A点的情况下,该离子回到A点所需的最短时间t.