时间:2019-06-23 22:35:23
1、计算题 甲车以加速度2m/s2由静止开始作匀加速直线运动，乙车落后4s在同一地点由静止开始，以加速度8m/s2作匀加速直线运动，两车的运动方向相同，求：
（1）在乙车追上甲车之前，两车距离的最大值是多少？
（2）乙车出发后经多长时间可追上甲车？此时它们离开出发点多远？
参考答案：解：（1）两车速度相同时间距最大，即
? 解得
? 两车间距：
（2）设经过t"乙车追上甲车，即
? 解得
，
（舍，因为此时甲还没出发）
? 距出发点距离：
64m
本题解析：
本题难度：一般
2、选择题 如图所示，在光滑的斜面上放置3个相同的小球（可视为质点），小球1、2、3距斜面底端A点的距离分别为x1，x2，x3，现将它们分别从静止释放，到达A点的时间分别为t1，t2，t3，斜面的倾角为θ，则下列说法正确的是（ ）
A．
| x1 t1 |
| x2 t2 |
| x3 t3 |
| x1 t1 |
| x2 t2 |
| x3 t3 |
| x1 t12 |
| x2 t22 |
| x3 t32 |
| x1 t21 |
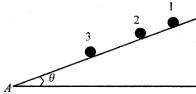
参考答案：如图，小球进行受力分析：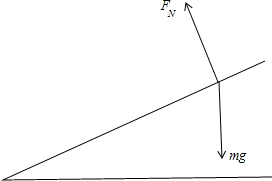
小球所受沿斜面向下的合力大小为F合=mgsinθ
即加速a=gsinθ
又根据题意可得：小球做初速度为0，加速度为a=gsinθ的匀加速直线运动，下滑距离和时间满足：
x=12at2
即位移xt2=12a
又因为三种情况下小球下滑的加速度相同，所以有：x1t21=x2t22=x3t23=12gisnθ，故C正确，D错误；
据：小球从斜面上下滑，做初速度为0的匀加速直线运动，据x=12at2知：
xt=12at
又t=
本题解析：
本题难度：简单
3、计算题 （16分）一滑块经水平轨道AB，进入竖直平面内的四分之一圆弧轨道BC。已知滑块的质量m=0.6kg，在A点的速度vA=8m/s，AB长x=5m，滑块与水平轨道间的动摩擦因数μ=0.15，圆弧轨道的半径R=2m，滑块离开C点后竖直上升h=0.2m，取g=10m/s2。
（不计空气阻力）求：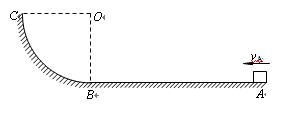
（1）滑块经过B点时速度的大小；
（2）滑块冲到圆弧轨道最低点B时对轨道的压力；
（3）滑块在圆弧轨道BC段克服摩擦力所做的功。
参考答案：（1）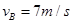
（2）
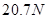，方向竖直向下（3）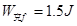
本题解析：（1）（6分）滑块从A到B，做匀减速直线运动，摩擦力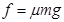
……1分
由牛顿第二定律可知，加速度大小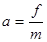
……2分
由运动学公式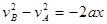
……2分
联立上式，解得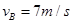……1分
（2）（4分）滑块冲到圆弧轨道最低点B时?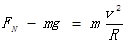
?……2分
滑块对轨道的压力?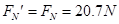
?……1分?
方向竖直向下? ……1分
（3）（ 6分）滑块离开C点后做竖直上抛运动，由运动学公式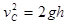
? ……2分
从B到C的过程中，克服摩擦力做功W克f，由动能定理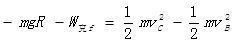
? ……3分
联立上式，解得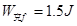? ……1分
本题难度：一般
4、选择题 不计空气阻力，一球从空中自由落下，碰到桌面立刻反弹，反弹前后瞬间的速度大小不变，取向上为速度的正方向，则该球的速度─时间图象应为下图中的（ ）
A．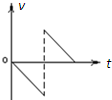
B．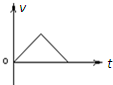
C．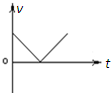
D．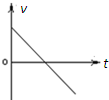
参考答案：小球自由下落，速度逐渐增大，碰到桌面时的速度方向向下，为负；反弹前后瞬间速度大小不变，速度反向，竖直向上，为正，且减速直线运动，故BCD错误，A正确．
故选A．
本题解析：
本题难度：简单
5、选择题 已知做匀变速直线运动的物体的位移随时间的变化关系为x=12t-3t2，根据这一关系式可知（ ）
A．v0=16m/s
B．v0=24m/s
C．a=-3m/s2
D．a=-6m/s2
参考答案：题中匀变速直线运动的物体的位移随时间的变化关系式x=12t-3t2，而匀变速直线运动的位移一般公式x=v0t+12at2，进行对比得到，v0=12m/s，a=-6m/s2．
故选D．
本题解析：
本题难度：简单