时间:2019-06-23 22:32:14
1、选择题 如图所示,一质量为M的木块与水平面接触,木块上方固定有一根直立的轻质弹簧,弹簧上端系一带电且质量为m的小球(弹簧不带电),在竖直方向上振动.当加上竖直方向的匀强电场后,在弹簧正好恢复到原长时,小球具有最大速度.在木块对水平面压力为零时,小球的加速度大小是( )
A.
| M+m m |
| M+m M |
| M m |
| m M |

参考答案:当小球加速度为零时,速度最大,此时mg=qE.当木块对水平面压力为零时,知弹簧的弹力为Mg,
电场力与重力的合力为零,小球所受的合力为Mg,根据牛顿第二定律有:a=Mmg.故C正确,A、B、D错误.
故选C.
本题解析:
本题难度:简单
2、计算题 (10分)如图所示,五块完全相同的长木板依次紧挨着放在水平地面上,每块木板的长度L=0.5m,质量m=0.6kg。一质量M=1kg的小物块以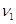 =3m/s水平速度从第一块长木板的最左端滑入。已知小物块与长木板间的动摩擦因数
=3m/s水平速度从第一块长木板的最左端滑入。已知小物块与长木板间的动摩擦因数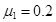 ,长木板与地面间的动摩擦因数
,长木板与地面间的动摩擦因数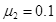 ,设最大静摩擦力与滑动摩擦力相等。重力加速度g取
,设最大静摩擦力与滑动摩擦力相等。重力加速度g取 。求:
。求: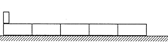 ?
?
(1)小物块滑至第四块长木板时,物块与第四块长木板的加速度分别为多大?
(2)物块在整个运动过程中相对出发点滑行的最大距离?
参考答案:(1)2m/s2?(2)2.27m
本题解析:(1)设当物块滑至第n块木板时,木板与地面的摩擦力小于小物块与木板的摩擦力,即
解得n>4.3
物块滑上第五块木板时,木板才开始在地面上滑动。
即:小物块滑至第四块长木板时,第四块长木板的加速度为零。
物块的加速度为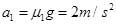
(2)设物块刚滑上第五块木板时的速度为 ,每块木板的长度为L,由动能定理
,每块木板的长度为L,由动能定理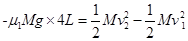
解得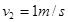
物块在第五块木板表面做匀减速直线运动,木板做匀加速直线运动,设经历时间t,物块与木板能获得相同的速度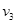 ,
,
对物块
 ?
?
对木板
 ?
?
解得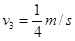
在此过程中,物块发生的位移为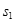 ,由动能定理
,由动能定理
解得
即物块与木板获得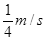 的共同速度,之后整体向前匀减速运动
的共同速度,之后整体向前匀减速运动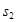 后静止.由动能
后静止.由动能
定理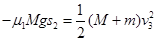
解得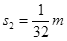
所以物块总共发生的位移
本题难度:一般
3、计算题 (10分)质量M=9kg、长L=1m的木板在动摩擦因数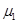 =0.1的水平地面上向右滑行,当速度
=0.1的水平地面上向右滑行,当速度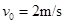 时,在木板的右端轻放一质量m=1kg的小物块如图所示.当小物块刚好滑到木板左端时,物块和木板达到共同速度.取g=10m/s2
时,在木板的右端轻放一质量m=1kg的小物块如图所示.当小物块刚好滑到木板左端时,物块和木板达到共同速度.取g=10m/s2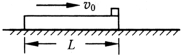
求:
(1)从木块放到木板上到它们达到相同速度所用的时间t;
(2)小物块与木板间的动摩擦因数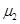 .
.
参考答案:(1)t=1s(2)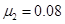
本题解析:(1)设木板在时间t内的位移为x1;木块的加速度大小为a2,时间t内的位移为x2
?则有x1= v0t- ?①
?①
x2=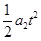 ?②
?②
x1= ?③
?③
又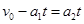 ?④
?④
你入数据得t=1s?⑤
(2)根据牛顿第二定律,有 ?⑥
?⑥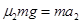 ?⑦
?⑦
解得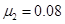 ?⑧
?⑧
评分标准:本题共10分,③⑥每式2分,其余每式1分
点评:本题难度较小,明确两物体的位移关系,由运动学规律求解
本题难度:一般
4、计算题 如图10甲所示,一根质量可以忽略不计的轻弹簧,劲度系数为k,下面悬挂一个质量为m的砝码A。手拿一块质量为M的木板B,用木板B托住A向上压缩弹簧到一定程度,如图乙所示。此时如果突然撤去木板B,则A向下运动的加速度a(a>g)。现用手控制使B以加速度a/3向下做匀加速直线运动。(1)求砝码A做匀加速直线运动的时间。(2)求出这段运动过程的起始和终止时刻手对木板B的作用力大小的表达式。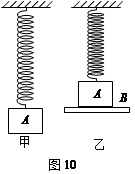
参考答案:(1)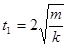 ;(2)M(g-a/3)。
;(2)M(g-a/3)。
本题解析:(1)设最初弹簧被压缩的长度为x0,根据牛顿第二定律对A有kx0+mg=ma
解得x0=m(a-g)/k
设A和B以加速度a/3向下做匀加速运动过程的终止时刻弹簧的压缩量为x1,根据牛顿第二定律对A有? kx1+mg=ma/3?
解得x1=m(a/3-g)/k
设A和B一起做匀加速运动的时间为t1,在这段时间内,A运动的位移为
s=x0-x1
根据s=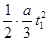 ,可解得
,可解得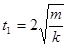 ?
?
(2)起始时刻A受三个力,满足mg+kx0-N1="ma/3"
B受三个力,满足Mg+N1-F1="Ma/3"
解得:F1=M(g-a/3)+2ma/3
A与B脱离时B受二个力,满足Mg-F2=Ma/3
解得:F2= M(g-a/3)
本题难度:一般
5、选择题 一质量为m的人站在匀加速竖直上升的电梯中,电梯上升的加速度大小为
| 1 4 |
| 1 4 |
| 3 4 |
| 5 4 |
参考答案:根据牛顿第二定律得,N-mg=ma,解得N=mg+ma=54mg.所以人对电梯的压力大小为54mg.故D正确,A、B、C错误.
故选D.
本题解析:
本题难度:简单