时间:2019-06-23 22:31:53
1、选择题 带电粒子(重力不计)以垂直于场的速度进入匀强电场或匀强磁场中时,粒子将发生偏转,这种电场或磁场称为偏转电场或偏转磁场. 下列说法中错误的是(?)
A.欲把速度不同的同种带电粒子分开,偏转电场或偏转磁场均可采用
B.欲把动能相同的质子和α粒子分开,只能采用偏转电场
C.欲把由静止经同一加速电压加速的质子和α粒子分开,偏转电场或偏转磁场均可采用
D.欲把初速度相同而比荷不同的带电粒子分开,偏转电场或偏转磁场均可采用
参考答案:C
本题解析:速度不同的粒子,在电场中相同时间内侧移距离相同而初速度方向的位移不同,可以分离,在磁场中轨道半径不同,也可以分离开,A项是对的;动能相同的质子和α粒子在电场中侧移距离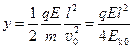 ,由于电荷量不同,可能分开,而在磁场中
,由于电荷量不同,可能分开,而在磁场中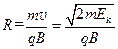 ,代入质量和电荷量得半径相同,不能分开,B是对的;由静止经同一加速电压加速后的质子和α粒子具有相同的动能,因此C错;由上述结论可知,初速度相同而比荷不同的带电粒子,偏转电场或偏转磁场均可分开,D项正确。选C。
,代入质量和电荷量得半径相同,不能分开,B是对的;由静止经同一加速电压加速后的质子和α粒子具有相同的动能,因此C错;由上述结论可知,初速度相同而比荷不同的带电粒子,偏转电场或偏转磁场均可分开,D项正确。选C。
本题难度:一般
2、计算题 如图所示,一个带电的小球从P点自由下落,P点距场区边界MN高为h,边界MN下方有方向竖直向下、电场强度为E的匀强电场,同时还有垂直于纸面的匀强磁场,小球从边界上的a点进入电场与磁场的复合场后,恰能做匀速圆周运动,并从边界上的b点穿出,已知ab=L,求: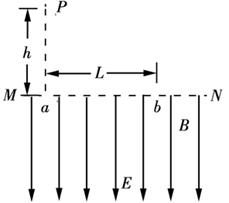
(1)小球的带电性质及其电荷量与质量的比值;
(2)该匀强磁场的磁感应强度B的大小和方向;
(3)小球从P经a至b时,共需时间为多少?
参考答案:(1) ?(2)
?(2)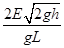 、方向垂直纸面向外?(3)
、方向垂直纸面向外?(3)
本题解析:(1)小球进入电场与磁场的复合场后,恰能做匀速圆周运动,则重力与电场力平衡,电场力方向向上,场强向下,小球带负电;
由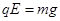 可得电荷量与质量的比值
可得电荷量与质量的比值
(2)粒子由a到b运动半周,由左手定则可得磁场方向垂直纸面向外;
由
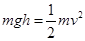
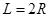
解得
(3)设小球下落h时间为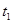 ,磁场中的运动时间为
,磁场中的运动时间为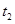
由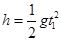 可得
可得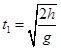
由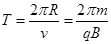
在磁场中运动时间为
则小球从P经a至b时,共需时间为
点评:带电粒子在复合场中做匀速圆周运动,则重力和电场力平衡,洛仑兹力提供做圆周运动的向心力。
本题难度:一般
3、计算题 (16分)如图所示,xoy平面内,y轴左侧有方向竖直向下,电场强度为E=1.0×1 04 N/的匀强电场。在Y轴右侧有一个边界为圆形的匀强磁场区域,圆心O’位于x轴上,半径为r=0.01 m,磁场最左边与Y轴相切于O点,磁感应强度为B=0.01T,方向垂直纸面向里。在坐标xo=0.06m处有垂直于x轴的足够大的荧光屏PQ。一束带正电的粒子从电场中的A点(图中未标出)以垂直于电场的初速度向右运动,穿出电场时恰好通过坐标原点,速度大小为v="2" ×106m/s,方向与x轴正向成300角斜向下。已知粒子的质量为m=1.0×l0-2kg,电量为q=1.0×10-10C,重力不计。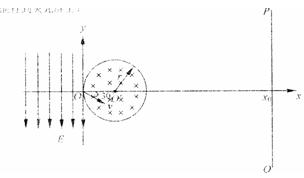
(1)求粒子出发点A的坐标;
(2)若圆形磁场可沿x轴向右移动,圆心O仍在x轴上,由于磁场位置的不同,导致该粒子打在荧光屏上的位置也不同,求粒子打在荧光屏上的位置范围;
(3)若改变磁场半径,磁场最左边仍然与Y轴相切于O点,当磁场半径至少为多大时,粒子就再也不能打到带屏上?
参考答案:
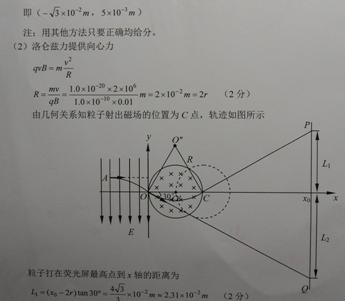

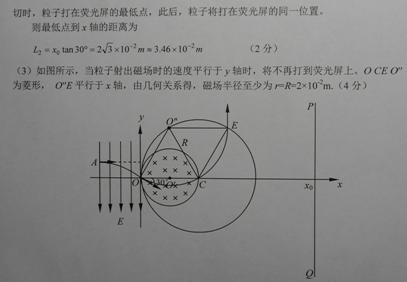
本题解析:略
本题难度:一般
4、选择题 如图所示,水平放置的平行金属板a、b带有等量异种电荷,a板带正电,两板间有垂直于纸面向里的匀强磁场,若一个带正电的液滴在两板间做直线运动,其运动方向是( )
A.沿竖直方向向下
B.沿竖直方向向上
C.沿水平方向向左
D.沿水平方向向右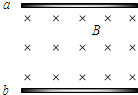
参考答案:
带正电的液滴在两板间作直线运动,可知粒子受力平衡,对液滴进行受力分析,受重力和洛伦兹力作用,重力方向竖直向下,洛伦兹力的方向只能向上,由左手定则可判断出带正电的液滴只能向右运动.因洛伦兹力大小不变,所以液滴只能做匀速直线运动.选项D正确,选项ABC错误.
故选D.
本题解析:
本题难度:一般
5、选择题 如图甲所示,在一条电场线上有A、B两点,若从A点由静止释放一电子,假设电子仅受电场力作用,电子从A点运动到B点的速度-时间图像如图乙所示,则(?)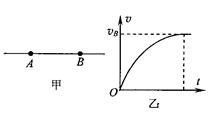
A. 电子在A、B两点受的电场力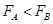 ?
?
B.A、B两点的电场强度相同
C.A、B两点的电势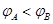
D.电子在A、B两点具有的电势能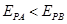
参考答案:C
本题解析:由v-t图像知,图线的斜率减小,则电子运动的加速度减小,由F=ma知电场力减小,即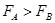 ,A错;由
,A错;由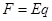 知场强减小,B错;因电子做加速运动,所以电场力是从A到B,场强方向为从B到A,因沿电场线方向电势降低,所以
知场强减小,B错;因电子做加速运动,所以电场力是从A到B,场强方向为从B到A,因沿电场线方向电势降低,所以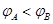 ,C对;因电子做加速运动,所以电场力做正功,电势能减小,即
,C对;因电子做加速运动,所以电场力做正功,电势能减小,即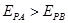 ,D错。
,D错。
点评:本题学生能从v-t图像判断出电子做加速度减小的加速运动,且电场力做正功。
本题难度:一般