时间:2019-06-23 22:08:31
1、简答题 如图所示，在一个水平向右运动的质量为M的车厢内，用一定滑轮通过一轻绳悬挂A、B两个物体。A的质量为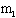
，B的质量为
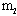，且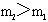
，B的悬绳在竖直方向上，A的悬绳向左偏离竖直方向θ角。两物体与车厢相对静止，滑轮的质量不计，求车厢地板对B物体的摩擦力和支持力的大小。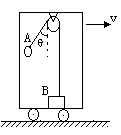
?
2、选择题 如图所示，光滑绝缘细杆AB，水平放置于被固定的带负电荷的小球的正上方，小球的电荷量为Q，可视为点电荷．a、b是水平细杆上的两点，且在以带负电小球为圆心的同一竖直圆周上．一个质量为m、电荷量为q的带正电的小圆环（可视为质点）套在细杆上，由a点静止释放，在小圆环由a点运动到b点的过程中，下列说法中正确的是?（ ）
A．小圆环所受库仑力的大小先增大后减小
B．小圆环的加速度先增大后减小
C．小圆环的动能先增大后减小
D．小圆环与负电荷组成的系统电势能先增大后减小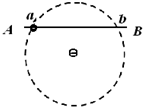
3、计算题 如图所示的传送带,其水平部分ab="2" m,倾斜bc="4" m,bc与水平面的夹角α=37°,物体A与传送带间的动摩擦因数μ=0.8.传送带沿如图所示的方向运动,速度大小始终为4 m/s,若将物体A(可视为质点)轻放于a处,它将被传送带运到c点,在此过程中,物体A一直没有脱离传送带,试求将物体从a点运动到c点所用的时间.(取g="10" m/s2)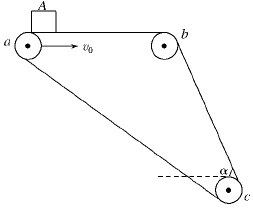
4、选择题 如图所示，在光滑水平面上有一质量为m1的足够长的木板，其上叠放一质量为m2的木块。假定木块和木板之间的最大静摩擦力和滑动摩擦力相等。现给木块施加一随时间t增大的水平力F＝kt(k是常数)，木板和木块加速度的大小分别为a1和a2。下列反映a1、a2变化的图线中正确的是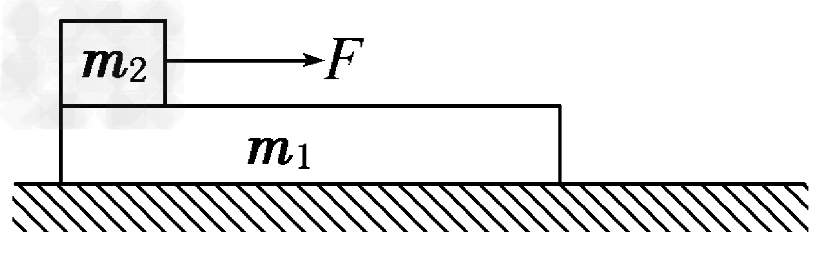
[? ]
A、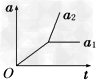
B、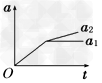
C、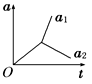
D、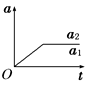
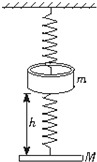
5、选择题 一轻质弹簧，上端悬挂于天花板，下端系一质量为M的平板，处在平衡状态．一质量为m的均匀环套在弹簧外，与平板的距离为h，如图所示，让环自由下落，撞击平板．已知碰后环与板以相同的速度向下运动，使弹簧伸长?（ ）
A．若碰撞时间极短，则碰撞过程中环与板的总动量守恒?
B．若碰撞时间极短，则碰撞过程中环与板的总机械能守恒?
C．环撞击板后，板的新的平衡位置与h的大小无关?
D．在碰后板和环一起下落的过程中，它们减少的动能等于克服弹簧力所做的功