时间:2019-06-23 21:24:31
1、选择题 如图所示,一导线弯成半径为a的半圆形闭合回路。虚线MN右侧有磁感应强度为B的匀强磁场。方向垂直于回路所在的平面。回路以速度v向右匀速进入磁场,直径C始终与MN垂直。从D点到达边界开始到C点进入磁场为止,下列结论不正确的是?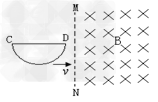
[? ]
A.感应电流方向不变?
B.CD段直线始终不受安培力?
C.感应电动势最大值E=Bav?
D.感应电动势平均值
参考答案:D
本题解析:
本题难度:一般
2、选择题 在如甲、乙、丙三图中,除导体棒ab可动外,其余部分均固定不动,甲图中的电容器C原来不带电,丙图中的直流电源电动势为E,除电阻R外,导体棒、导轨和直流电源的电阻均可忽略,导体棒和导轨间的摩擦也不计.图中装置均在水平面内,且都处于方向垂直水平面(即纸面)向下的匀强磁场中,导轨足够长.今给导体棒ab一个向右的相同初速度v0,以下说法正确的是( )
A.在导体棒刚开始运动时,甲、乙、丙三种情况中通过电阻R的电流相同
B.三种情形下导体棒ab最终都将静止
C.最终只有乙中导体棒ab静止,甲、丙中导体棒ab都将作匀速直线运动
D.在导体棒ab运动的全部过程中,三个电阻R产生的热量大小是Q甲>Q乙>Q丙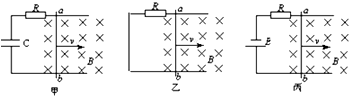
参考答案:A、导体棒刚开始运动时,导体棒产生的感应电动势为 E0=BLv0,甲、乙中,感应电流都为:I=E0R=BLv0R
丙图中,感应电动势方向与电池的电动势方向相同,电路中的电流:I=E+E0R,大于甲、乙中的电流.故A错误.
B、C、图甲中,导体棒向右运动切割磁感线产生感应电流而使电容器充电,当电容器C极板间的电压与导体棒产生的感应电动势相等时,电路中没有电流,ab棒不受安培力,向右做匀速运动;
图乙中,导体棒向右运动切割磁感线产生感应电流,通过电阻R转化为内能,ab棒速度减小,当ab棒的动能全部转化为内能时,ab棒静止;
图丙中,导体棒先受到向左的安培力作用向右做减速运动,速度减为零后再在安培力作用下向左做加速运动,当导体棒产生的感应电动势与电源的电动势相等时,电路中没有电流,ab棒向左做匀速运动.故B错误,C正确.
D、甲中棒的部分动能转化为内能,图乙图过程中,棒的动能全部转化为内能;丙图中,电源的电能和棒的动能转化为内能,故有Q甲<Q乙<Q丙.故D错误.
故选:C
本题解析:
本题难度:简单
3、选择题 如图所示,用均匀导线做成一个正方形线框,每边长为0.2m,正方形的一半放在和线框垂直的垂直纸面向里的匀强磁场中,当磁场的变化为每0.1s增加1T时,线框中点a、b两点的电势差是( )
A.Uab=0.1V
B.Uab=-0.1V
C.Uab=0.2V
D.Uab=-0.2V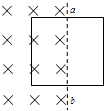
参考答案:由楞次定律可以判断,当线框中的磁场增加时,感应电流的磁场与原磁场方向相反,为垂直于纸面向外,由安培定则可以判断出感应电流的方向为逆时针方向,所以b点电势高于a点电势.
根据法拉第电磁感应定律得 感应电动势 E=△B△tS,
其中S=12L2,磁场的变化为每0.1s增加1T时,△B△t=10T/s,
解得E=0.2V
由闭合电路欧姆定律ab电势差U=IR=0.1V,由于b点电势高于a点电势,所以Uab=-0.1 V,
故选B.
本题解析:
本题难度:简单
4、选择题 如图所示,一有界匀强磁场,磁感应强度大小均为B,方向分别垂直纸面向里和向外,磁场宽度均为L,在磁场区域的左侧相距为L处,有一边长为L的正方形导体线框,总电阻为R,且线框平面与磁场方向垂直.现使线框以速度v匀速穿过磁场区域.若以初始位置为计时起点,规定电流逆时针方向时的电流和电动势方向为正,B垂直纸面向里时为正,则以下四个图象中对此过程描述不正确的是( )
A.
B.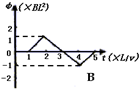
C.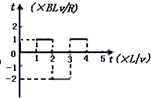
D.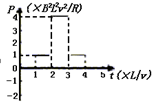
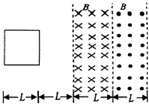
参考答案:当线框运动L时,右边开始切割磁感线,产生E=BLv的电动势,电路中电流I=BLvR; 当向右再运动L时,线框两边均切割磁感线,由于磁场反向,故电动势E′=2BLv,此时电流的方向反向,电流I′=2BLvR;当线圈再向右运动L过程中,只有左侧切割磁感线,此时,电动势为E=BLv,方向沿正方向,故AC正确;
电路中功率P=E2R,故D正确;
线圈在运动过程中,L-2L处时磁通量均匀增大,而2L-3L过程中,由于内外磁通量相互抵消,故磁通量在2.5L处应为零,故B错误;
本题选错误的,故选B.
本题解析:
本题难度:简单
5、简答题 不计电阻的光滑平行轨道EFG、PMN构成相互垂直的L型,磁感应强度为B的匀强磁场方向与水平的EFMP平面夹角θ(θ<45°)斜向上,金属棒ab、cd的质量均为m、长均为L、电阻均为R.ab、cd由细线通过角顶处的光滑定滑轮连接,细线质量不计,ab、cd与轨道正交,已知重力加速度为g.
(1)求金属棒的最大速度vmax;
(2)当金属棒速度为v时,且v小于最大速度vmax时,求机械能损失的功率P1和电阻的发热功率P2.
参考答案:(1)金属棒达到最大速度vmax时,回路中的感应电动势为:E=BLvmaxcosθ-BLvmaxsinθ
回路中感应电流:I=E2R
当两棒均做匀速运动时,棒的速度达最大值,故有:
mg=BILcosθ-BILsinθ
联立得:vmax=2mgRB2L2(cosθ-sinθ)2.
(2)当金属棒速度为v时,且v小于最大速度vmax时,机械能损失的功率P1等于电阻的发热功率P2,且均为:P1=P2=E′22R=B2L2v2(cosθ-sinθ)22R
答:(1)金属棒的最大速度vmax为2mgRB2L2(cosθ-sinθ)2.
(2)当金属棒速度为v时,且v小于最大速度vmax时,机械能损失的功率P1为B2L2v2(cosθ-sinθ)22R,电阻的发热功率P2为B2L2v2(cosθ-sinθ)22R.
本题解析:
本题难度:一般