时间:2019-06-23 21:24:31
1、选择题 如图所示，在竖直向下的匀强磁场中，将一水平放置的金属棒ab以水平初速度v0抛出，设在整个过程中棒的方向不变且不计空气阻力，则在金属棒运动过程中产生的感应电动势大小变化情况是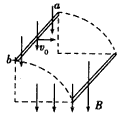 
[? ]
A．越来越大
B．越来越小
C．保持不变
D．无法判断
参考答案：C
本题解析：
本题难度：简单
2、简答题 如图所示，在光滑的水平面上有两个方向相反的匀强磁场垂直穿过，磁场的宽度均为L，磁感应强度大小均为B，水平面上放有一正方形金属线框，其边长为a（a＜L），电阻为R．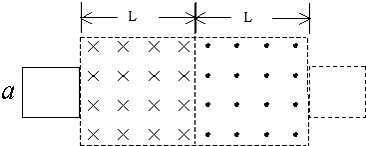
（1）若线框以速度v从磁场区左侧匀速向右穿过该磁场区域到达磁场区右侧的过程中，求外力所做的功．
（2）若线框从磁场区左侧以水平向右的某个初速度进入磁场，刚好能从磁场区右侧全部出来，求线框在进入磁场和离开磁场的过程中产生的热量之比．
参考答案：（1）线圈进入磁场的过程中，安培力做功
? W1=F1a=（I1aB）a=(BavRaB)a=B2a3vR
线圈从左侧磁场进入右侧磁场的过程中，
安培力做功W2=F2a=（2I2aB）a=（22BavRaB）a=4B2a3vR
线圈离开磁场的过程中，安培力做功
? W3=F3a=（I3aB）a=（BavRaB）a=B2a3vR
整个过程中外力做功等于安培力做的总功
?W=W1+W2+W3=6B2a3vR
（2）设线圈进入磁场前的初速度为v0，在左侧磁场中运动的速度为v1，线圈在右侧磁场中运动的速度为v2，线圈的质量为m
线圈在进入磁场过程中，根据动量定理得：
-.F1t1=-（.I1aB）t1=mv1-mv0
又感应电荷量q1=.I1t1．
即-q1aB=mv1-mv0?①
线圈从左侧磁场进入右侧磁场的过程中，同理可得：
-2F2t2=-2（.I2aB）t2=mv2-mv1
即-2q2aB=mv2-mv1 ②
线圈离开磁场的过程中，同理可得：
-.F3t3=-（.I3aB）t3=-mv2
即-q3aB=0-mv2 ③
又感应电荷量q1=△Φ1R，q2=△Φ2R，q3=△Φ3R
其中△Φ1=△Φ2=Ba2，△Φ3=2Ba2，
所以q2=2q1，q3=q1
由①②③式解得v1=56v0，v2=16v0
所以Q1Q2=12mv20-12mv2112mv22-0=v20-v21v22=111
答：
（1）外力所做的功为6B2a3vR．
（2）线框在进入磁场和离开磁场的过程中产生的热量之比为11：1．
本题解析：
本题难度：一般
3、简答题 如图所示，由10根长度都是L的金属杆，连接成一个“目”字型的矩形金属框abcdefgha，放在纸面所在的平面内；有一个宽度也为L的匀强磁场，磁场边界跟de杆平行，磁感强度的大小是B，方向垂直于纸面向里，水平金属杆ab、bc、cd、ef、fg和gh的电阻不计，其他各杆的电阻都为R，各杆端点间接触良好．现在以速度v匀速把金属框从磁场的左边界向右拉，当de杆刚进入磁场时，开始计时，求：（1）从开始计时到ah杆刚要进入磁场的过程中，通过ah杆某一横截面上的总电量．（2）从开始计时到金属框全部通过磁场的过程中，金属框中电流所产生的总热量．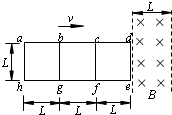
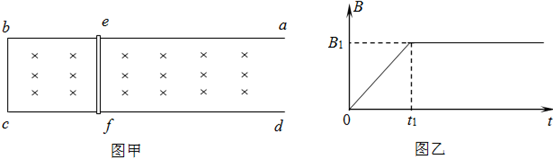
参考答案：（1）总电阻R=r3+r=4r3；
金属框干路中的电流I=BLvR；
通过ah杆的电流I′=I3
从开始计时以ah杆刚进入磁场的时间t=3Lv；
在这段时间内通过ah杆的总电荷量q=I′t；
联立解以上各式解得：q=3BL24r
（2）匀速拉动金属框时，根据平衡条件得
外力F=FB=BIL；
根据能量守恒定律得：在这一过程中电流产生的热量Q=W=Fs，式中s=4L；
联立以上等式解得：Q=3B2L3vr
答：（1）从开始计时到ah杆刚要进入磁场的过程中，通过ah杆某一横截面上的总电量是3BL24r．
（2）从开始计时到金属框全部通过磁场的过程中，金属框中电流所产生的总热量是3B2L3vr．
本题解析：
本题难度：一般
4、简答题 如图甲所示，固定于水平桌面上的金属导轨abcd足够长，金属棒ef搁在导轨上，可无摩擦地滑动，此时bcfe构成一个边长为l的正方形．金属棒的电阻为r，其余部分的电阻不计．在t=0的时刻，导轨间加一竖直向下的磁场，磁感应强度随时间的变化如图乙所示．为使金属棒ef在0-t1保持静止，在金属棒ef上施加一水平拉力F，从t1时刻起保持此时的水平拉力F不变，金属棒ef在导轨上运动了s后刚好达到最大速度，求：
（1）在t=
| t1 2 |
参考答案：（1）t12时刻，感应电动势E=△B△tS=B1l2t1，
导体棒受到的安培力F安=B12?I?l=B12?B1l2t1r?l=B21l32rt1，
由楞次定律可知，感应电流从f流向e，由左手定则可知，导体棒受到的安培力向左；
由平衡条件可知，此时水平拉力F=B21l32rt1，方向水平向右；
（2）导体棒切割磁感线产生感应电动势，
当金属棒的速度最大时，感应电动势E′=B1lvm，
此时导体棒受到的安培力F安′=B1?B1lvmr?l，
此时水平拉力F′=2×B21l32rt1=B21l3rt1，
当安培力与拉力合力为零时，导体棒做匀速直线运动，此时速度最大，
即：F′=F安′，B21l3rt1=B1?B1lvmr?l；
解得，导体棒的最大速度：vm=lt1；
（3）金属棒静止时的感应电流：I?1=B1l2rt1，
产生的焦耳热：Q1=I21rt1=B21l4rt1，
金属棒从开始运动到最大速度阶段，
由能量守恒定律，得：Q2=Fs-12mv2m=B21l3rt1?s-12m(lt1)2=B21l3srt1-ml22t21，
全过程产生的焦耳热Q=Q1+Q2=B21l3(l+s)rt1-ml22t21；
答：（1）在t=t12时刻该水平拉力F的大小为B21l32rt1，方向水平向右；
（2）金属棒ef在导轨上运动的最大速度是lt1；
（3）从t=0开始到金属棒ef达到最大速度的过程中，金属棒ef中产生的热量是B21l3(l+s)rt1-ml22t21．
本题解析：
本题难度：一般
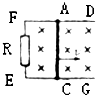
5、选择题 如图所示，一导线AC以速度υ在金属轨道DFEF上匀速滑动，向右通过一匀强磁场，金属轨道EF间有电阻R，其余的电阻不计，则在通过此匀强磁场的过程中，下列物理量中与速度υ成正比的是：（ ）
①导线AC中的感应电流强度
②磁场作用于导线AC上的磁场力
③电阻R上所产生的电热
④电阻R上所消耗的电功率．
A．①②
B．①③
C．②④
D．③④
参考答案：①AC产生的感应电动势 E=BLv，感应电流为 I=ER=BLvR∝v，故①正确．
②磁场作用于导线AC上的磁场力：F=BIL=B2L2Rv∝v，故②正确．
③根据能量转化和守恒定律得知，电阻R上所产生的电热为 Q=Fs=B2L2Rvs∝v，故③正确．
④电阻R上所消耗的电功率：P=E2R=(BLv)2R∝v2，故④错误．
故选：AB
本题解析：
本题难度：简单