时间:2019-05-21 05:34:25
1、选择题 粗糙水平面上一物体以一定初速度向前滑行，从开始滑行到停止，物体的运动位移为S，运动时间为t，运动过程中的加速度大小为a，则下列说法正确的是
A．运动位移S随初速度增大而增大，随质量增大而减小
B．运动时间t随初速度增大而增大，与质量无关
C．加速度大小a随质量增大而减小
D．位移S、运动时间t、加速度大小a都随初速度增大而增大
参考答案：B
本题解析：略
本题难度：一般
2、选择题 空间内有两个沿竖直方向的有界匀强磁场I、II，磁感应强度大小均为B，宽度均为L，边界线平行，磁场I竖直向下，磁场II竖直向上，如图所示为俯视图．一边长为L、质量为m的正方形导线框abcd放在光滑绝缘的水平面上，在水平恒力F作用下沿水平面通过两个磁场区域．线框的bc边始终平行于磁场区的边界，力F垂直于bc边，当bc边进入磁场I时，线框恰以速度v0做匀速运动，此时线框中的电流为i0；当ad边将要离开磁场II时线框中的电流稍小于i0，则（ ）
A．bc边在磁场II中运动时线框中的电流方向为adcba
B．bc边恰进入磁场II时线框的加速度大小为
| 3F m |
| v0 2 |
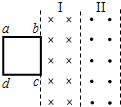
参考答案：A、bc边在磁场II中运动时，ad和bc两边都切割磁感线，根据右手定则判断得知线框中感应电流方向为abcda．故A错误．
B、bc边恰进入磁场II时线框中感应电动势为E=2BLv0，感应电流为i=ER，安培力为FA=2BiL，得FA=4B2L2v0R
而bc进入磁场I的过程中，有F=B2L2v0R．则得FA=4F．根据牛顿第二定律得：FA-F=ma，解得bc边恰进入磁场II时线框的加速度大小为a=3Fm．故B正确．
D、ad边将要离开磁场II时线框中的电流稍小于i0，线框的速度小于v0，线框bc边恰进入磁场II时速度为v0，线框又做减速运动，所以bc边在磁场II中运动的过程中线框中电流的最小值一定小于i0．故D正确．
C、若bc边恰离开磁场II时线框的速度大小为v02．线框中产生的感应电流为i=2BL?v02R=i0，而bc边在磁场II中运动的过程中线框中电流的最小值一定小于i0．故C错误．
故选BD
本题解析：
本题难度：一般
3、简答题 如图所示，A、B两个物体靠在一起放在光滑水平面上，它们的质量分别为MA=3kg，MB=6kg．今用水平力FA推A，用水平力FB拉B，FA和FB随时间变化的关系是FA=9-2t（N）、FB=3+2t（N）．求：
（1）从t=0到A、B脱离前，它们的加速度是多少？
（2）从t=0到A、B脱离时，物体A的位移是多少？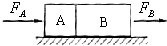
参考答案：（1）以A、B整体为对象：
FA+FB=（mA+mB）a
解得：a=43m/s2
（2）A、B脱离时，之间的弹力为零，对物体A，根据牛顿第二定律，有：
FA=mAa=4=9-2t
解得：t=2.5s?
从t=0到A、B脱离时，整体做匀加速直线运动，根据位移时间关系公式，有：
x=12at2=12×43×2．52m=256m
答：（1）从t=0到A、B脱离前，它们的加速度是43m/s2；
（2）从t=0到A、B脱离时，物体A的位移是256m．
本题解析：
本题难度：一般
4、选择题 如图所示，固定斜面的倾角为30°，现用平行于斜面的力F拉着质量为m的物体沿斜面向上运动，物体的加速度大小为a，若该物体放在斜面上沿斜面下滑时的加速度大小也为a，则力F的大小是( )．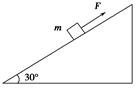
A．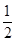
mg
B．
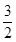mg
C．Mg
D．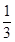
mg
参考答案：C
本题解析：据题意，向上拉时，物体向上做匀加速直线运动，则有：F－mgsin 30°－Ff＝ma，物体放在斜面上下滑时也做匀加速直线运动，则有：mgsin 30°－Ff＝ma，解得F＝mg，所以C项正确．
本题难度：一般
5、计算题 （10分）一质量为m ="40" kg的小孩站在电梯内的体重计上.电梯从t =0时刻由静止开始上升,在0到6 s内体重计示数F的变化如图所示.试问：在这段时间内电梯上升的高度是多少？取重力加速度g="10" m/s2.
参考答案：9（m）
本题解析：选取小孩为研究对象，地面为参考系，小孩受到重力和体重计对小孩的弹力，如图所示.小孩的运动分为三个阶段.在0~2s内以加速度a1向上做匀加速直线运动，根据牛顿第二定律可得，加速度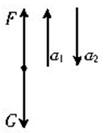
a1=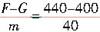
=1（m/s2）
根据匀变速直线运动公式可得，第一阶段位移s1=1/2a1t12=1/2×1×22=2（m）
第一阶段末速度
v1=a1t1=1×2=2（m/s）
2s~5s内向上以速度v1做匀速直线运动，根据匀速直线运动公式可得，第二阶段位移?
s2=v1t2=2×3=6（m）
在5s~6s内以加速度a2向上做匀减速直线运动，根据牛顿第二定律可得，加速度
a2=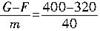
=2（m/s2）
设从速度v1减速为0的时间为t3，根据匀变速直线运动公式可得t3=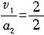
=1（s）
则可判断小孩子在第6s末速度为0，第三阶段位移
s3=v1t3-1/2a2t32=2×1-1/2×2×12=1（m）
则在这段时间内小孩上升的高度，即电梯上升的高度
s=s1+s2+s3=2+6+1=9（m）
点评：难度中等，本题为多过程问题，注意把整个过程分解为独立分析的分过程，联系分过程的桥梁就是速度，结合牛顿第二定律和运动学公式求解
本题难度：一般