时间:2019-05-21 05:34:25
1、选择题 如图所示,长方体物块C置于水平地面上,物块A、B用不可伸长的轻质细绳通过滑轮连接(不计滑轮与绳之间的摩擦),A物块与C物块光滑接触,整个系统中的A、B、C三物块在水平恒定推力F作用下从静止开始以相同的加速度一起向左运动。下列说法正确的是
[? ]
A、B与C之间的接触面可能是光滑的
B、若推力F增大,则绳子对B的拉力必定增大
C、若推力F增大,则定滑轮所受压力必定增大
D、若推力F增大,则C物块对A物块的弹力必定增大
参考答案:AD
本题解析:
本题难度:一般
2、选择题 如图所示,小球质量为m,被三根质量不计的弹簧A、B、C拉住,弹簧间的夹角均为120°,小球平衡时, A、B、C的弹力大小之比为3:3:1,当剪断C瞬间,小球的加速度大小及方向可能为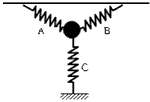
[? ]
A.g/2,竖直向下
B.g/2,竖直向上
C.g/4,竖直向上
D.g/4,竖直向下
参考答案:BD
本题解析:
本题难度:一般
3、选择题 如图所示,空间存在着与圆台母线垂直向外的磁场,各处的磁感应强度大小均为B,圆台母线与竖直方向的夹角为θ。一个质量为m、半径为r的匀质金属圆环位于圆台底部。圆环中维持恒定的电流I,圆环由静止向上运动,经过时间t后撤去该恒定电流并保持圆环闭合,圆环上升的最大高度为H。已知重力加速度为g,磁场的范围足够大。在圆环向上运动的过程中,下列说法正确的是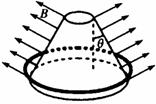
A.安培力对圆环做的功为mgH
B.圆环先做匀加速运动后做匀减速运动
C.圆环运动的最大速度为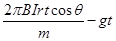
D.圆环先有扩张后有收缩的趋势
参考答案:C
本题解析:将磁场分解为水平向四周方向的和竖直向上的,通电圆环受安培力向上,可判断电流方向(从上向下看)为顺时针方向,根据左手定律,此时竖直向上的分磁场有使线圈收缩的趋势,D错误,水平向四周的分磁场对线圈有竖直向上的作用力,大小为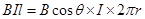 ,此时线圈向上做匀加速运动,线,加速度
,此时线圈向上做匀加速运动,线,加速度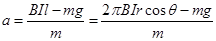 ,经过时间t,撤去恒定电流瞬间,此时速度达到最大,为
,经过时间t,撤去恒定电流瞬间,此时速度达到最大,为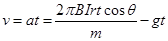 ,C正确;此后线圈再向上运动,会产生逆时针方向的感应电流,会受到向下的安培力,而且越向上运动,速度越小,安培力越小,因此做变减速运动,B错误;根据动能定理,在上升的整个过程中,
,C正确;此后线圈再向上运动,会产生逆时针方向的感应电流,会受到向下的安培力,而且越向上运动,速度越小,安培力越小,因此做变减速运动,B错误;根据动能定理,在上升的整个过程中,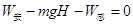 ,因此
,因此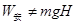 ,A错误。
,A错误。
本题难度:一般
4、选择题 如图所示,一轻弹簧左端固定在长木板m2的左端,右端与小木块m1连接,且m1、m2及m2与地面之间接触面光滑,开始时m1和m2均静止,现同时对m1、m2施加等大反向的水平恒力F1和F2,从两物体开始运动以后的整个过程中,对m1、m2和弹簧组成的系统(整个过程中弹簧形变不超过其弹性限度),下列说法正确的是(? )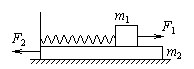
A.由于F1、F2等大反向,故系统机械能守恒
B.由于F1、F2分别对m1、m2做正功,故系统动能不断增加
C.由于F1、F2分别对m1、m2做正功,故系统机械能不断增加
D.当弹簧弹力大小与F1、F2大小相等时,m1、m2的动能 91ExAm.org最大
参考答案:D
本题解析:由于F1、F2对系统做功之和不为零,故系统机械能不守恒,故A错误;开始时,弹簧的弹力小于F1、F2,两物块加速,动能增加,当弹簧弹力大小与F1、F2大小相等时,M和m受力平衡,加速度减为零,此后速度减小,动能减小,故B错误;由于F1、F2先对系统做正功,当两物块速度减为零时,弹簧的弹力大于F1、F2,之后,两物块再加速相向运动,F1、F2对系统做负功,系统机械能开始减少,故C错误;当弹簧弹力大小与F1、F2大小相等时,M和m受力平衡,加速度减为零,此时速度达到最大值,故各自的动能最大,故D正确.
本题难度:一般
5、选择题 如图所示,一个重力G=4N的物体放在倾角为30°的光滑斜面上,斜面放在台秤上,当烧断细线后,物块正在下滑的过程中与稳定时比较,台秤示数( )
A.减小2?N
B.减小1?N
C.增大2?N
D.增大1?N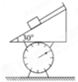
参考答案:设斜面的重力为G.整个装置保持静止状态时,台秤的示数为F1=GA+G.当细线被烧断物块正在下滑时,物块对斜面的压力大小为N=GAcos30°,对斜面研究得到,台秤的示数为F2=G+Ncos30°=G+34GA,故台秤的示数减小量为△F=GA-34GA=1N.
故选B.
本题解析:
本题难度:简单