时间:2019-05-21 05:29:06
1、简答题 如图所示,PQMN与CDEF为两根足够长的固定平行金属导轨,导轨间距为L.PQ、MN、CD、EF为相同的弧形导轨;QM、DE为足够长的水平导轨.导轨的水平部分QM和DE处于竖直向上的匀强磁场中,磁感应强度为B.a、b为材料相同、长都为L的导体棒,跨接在导轨上.已知a棒的质量为m、电阻为R,a棒的横截面是b的3倍.金属棒a和b都从距水平面高度为h的弧形导轨上由静止释放,分别通过DQ、EM同时进入匀强磁场中,a、b棒在水平导轨上运动时不会相碰.若金属棒a、b与导轨接触良好,且不计导轨的电阻和棒与导轨的摩擦.
(1)金属棒a、b刚进入磁场时,回路中感应电流的方向如何?
(2)通过分析计算说明,从金属棒a、b进入磁场至某金属第一次离开磁场的过程中,电路中产生的焦耳热.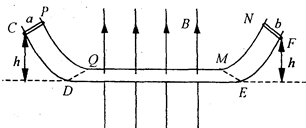
2、简答题 如图甲所示,电阻不计,间距为l的平行长金属导轨置于水平面内,阻值为R的导体棒ab固定连接在导轨左端,另一阻值也为R的导体棒ef垂直放置到导轨上,ef与导轨接触良好,并可在导轨上无摩擦移动.现有一根轻杆一端固定在ef中点,另一端固定于墙上,轻杆与导轨保持平行,ef、ab两棒间距为d.若整个装置处于方向竖直向下的匀强磁场中,且从某一时刻开始,磁感应强度B随时间t按图乙所示的方式变化.
(1)求在0~t0时间内流过导体棒ef的电流的大小与方向;
(2)求在t0-2t0时间内导体棒ef产生的热量;
(3)1.5t0时刻杆对导体棒ef的作用力的大小和方向.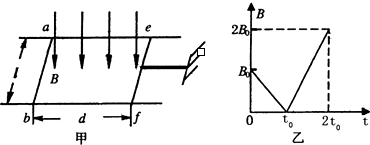
3、选择题 如图所示,闭合金属线圈abcd位于水平方向匀强磁场的上方h处,由静止开始下落,并进入磁场,在运动过程中,线框平面始终和磁场方向垂直,不计空气阻力,那么线框在进入磁场的过程中出现( )
A.可能加速运动
B.一定减速运动
C.可能匀速运动
D.可能静止状态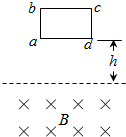
4、计算题 图中MN和PQ为竖直方向的两平行长直金属导轨,间距l为0.40m,电阻不计。导轨所在平面与磁感应强度为B=0.50T的匀强磁场垂直。质量为m=6.0×10-3 kg、电阻为r=1.0Ω的金属杆ab始终垂直于导轨,并与其保持光滑接触。导轨两端分别接有滑动变阻器和阻值为3.0Ω的电阻R1。当杆ab达到稳定状态时以速率v匀速下滑,整个电路消耗的电功率为P=0.27W,重力加速度g取10m/s2,试求速率v和滑动变阻器接入电路部分的阻值R2。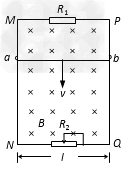
5、简答题 不计电阻的光滑平行轨道EFG、PMN构成相互垂直的L型,磁感应强度为B的匀强磁场方向与水平的EFMP平面夹角θ(θ<45°)斜向上,金属棒ab、cd的质量均为m、长均为L、电阻均为R.ab、cd由细线通过角顶处的光滑定滑轮连接,细线质量不计,ab、cd与轨道正交,已知重力加速度为g.
(1)求金属棒的最大速度vmax;
(2)当金属棒速度为v时,且v小于最大速度vmax时,求机械能损失的功率P1和电阻的发热功率P2.