时间:2019-05-21 05:22:18
1、选择题 做匀变速直线运动的质点，它的位移随时间变化的规律是x＝(24t－1.5t2)m，则质点的速度为零的时刻是( ) ?
A．1.5s
B．8s
C．16s
D．24s
参考答案：B
本题解析：根据待定系数法，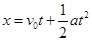
则，初速度为24m/s，加速度为-3m/s2。所以根据
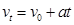可知，速度为零时刻为8s。
点评：此类题型考察了匀变速直线运动规律，通过待定系数法求出初速度，加速度，然后再求出时间
本题难度：一般
2、计算题 汽车以加速度为2m/s2的启动加速度由静止开始作匀加速直线运动，运动时间为3秒，然后以1m/s2的制动加速度减速前进，直到停下来。求：
（1）汽车前3秒的位移
（2）汽车总位移
参考答案：9米（2分）；27米（4分）
本题解析：略
本题难度：简单
3、选择题 某航母跑道长200m。飞机在航母上滑行的最大加速度为6m/s2，起飞需要的最小速度为50m/s。那么，飞机在滑行前，需要借助弹射系统获得的最小初速度为（ ）
A．20m/s
B．15m/s
C．10m/s
D．5m/s
参考答案：C
本题解析：根据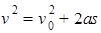
，则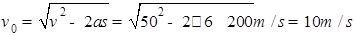
，选项C正确；
考点：匀变速直线运动的规律.
本题难度：一般
4、简答题 如图所示，平板车质量为m，长为L，车右端（A点）有一个质量为M=2m的小滑块（可视为质点）．平板车静止于光滑水平面上，小车右方足够远处固定着一竖直挡板，小滑块与车面间有摩擦，并且在AC段、CB段动摩擦因数不同，分别为μ1、μ2，C为AB的中点．现给车施加一个水平向右的恒力，使车向右运动，同时小物块相对于小车滑动，当小滑块滑至C点时，立即撤去这个力．已知撤去这个力的瞬间小滑块的速度为v0，车的速度为2v0，之后小滑块恰好停在车的左端（B点）与车共同向前运动，并与挡板发生无机械能损失的碰撞．试求：
（1）μ1和μ2的比值．
（2）通过计算说明，平板车与挡板碰撞后，是否还能再次向右运动．
参考答案：设在有水平外力F时平板车的加速度为a1，在无水平外力F时平板车的加速度为a2，小滑块在AC段和CB段的加速度分别为?a/1和a/2
由牛顿第二定律得：μ1?2mg=2m?a"1解得：a/1=μ1g①
同理：a/2=μ2g②
当小滑块在AC段运动时，由题意可知：
2v02t1-v02t1=L2③
v0=a/1t1④
由①③④联立得：v20=μ1gL⑤
设小滑块滑到B端时与车的共同速度为v1，由于滑块从C滑到B的过程中，滑块和车的系统受到的合外力为零，故动量守恒，于是有：
2m?v0+m?2v0=（2m+m）v1⑥
当小滑块在在CB段运动时，由运动学知识可知：
2v0+v12t2-v0+v12t2=L2
v1-v0=a/2t2⑧
由②⑥⑦⑧联立得：v20=3μ2gL⑨
所以，由⑤⑨得：μ1μ2=31
（2）设小滑块滑到B端时与车的共同速度为v1，由于滑块从C滑到B的过程中，滑块和车的系统受到的合外力为零，故动量守恒，于是有：
2m?v0+m?2v0=（2m+m）v1①
平板车与挡板碰撞后以原速大小返回，之后车向左减速，滑块向右减速，由于M=2m，所以车的速度先减小到零．设车向左运动的速度减小为零时，滑块的速度为v2，滑块滑离车B端的距离为L1．
由于上述过程系统的动量守恒，于是有：2m?v1-mv1=2m?v2②
对车和滑块的系统运用能量守恒定律得：
μ2?2m?gL2+μ1?2m?g(L1-L2)=12(2m+m)v21-12?2m?v22③
由①②③式及μ1gL=v20、μ2gL=13v20
可解得：L1=139L
由于L1=139L＞L，故小车的速度还没有减为零时，小物块已经从小车的右端滑下，之后小车向左匀速运动，故车不会再向右运动了
答：（1）μ1μ2=31；
（2）平板车与挡板碰撞后，不再向右运动．
本题解析：
本题难度：一般
5、选择题 初速度为0的匀变速直线运动，第1第2两秒，第3第4两秒，第5第6两秒内的位移之比为（ ）
A．1：2：3
B．1：3：5
C．1：4：9
D．以上都不对
参考答案：第1第2两秒，第3第4两秒，第5第6两秒内，时间相等且连续，初速度为零，则位移之比为1：3：5．故B正确，A、C、D错误．
故选B．
本题解析：
本题难度：简单