时间:2019-05-21 04:05:10
1、简答题 如图为一真空示波管的示意图,电子从灯丝K发出(初速度可忽略不计),经灯丝与A板间的电压U1加速,从A板中心孔沿中心线KO射出,然后进入两块平行金属板M、N形成的偏转电场中(偏转电场可视为匀强电场),电子进入M、N间电场时的速度与电场方向垂直,电子经过电场后打在荧光屏上的P点.?已知M、N两板间的电压为U2,两板间的距离为d,板长为L,电子的质量为m,电荷量为e,不计电子受到的重力及它们之间的相互作用力.
(1)求电子穿过A板时速度的大小v0;
(2)求电子从偏转电场射出时的侧移量y;
(3)若要使电子打在荧光屏上P点的上方,加速电压U1和M、N两板间的电压为U2将如何改变?(不用说明理由)
2、计算题 如图所示,沿水平方向有一匀强电场,在该电场中,用不可伸长的长为L的绝缘细绳一端拴一个带电小球,另一端固定在O点。已知带电小球所受重力是其受电场力的3/4倍,且小球恰能在平行于电场方向的竖直平面内做圆周运动。求小球在最低点A处速度的大小和运动过程中最大速度的大小。
3、简答题 如图所示,光滑轨道AB平直,BC部分是处于竖直平面内半径R的光滑半圆.圆心O处有一绝缘平台,一带正电小球被固定在圆心.另一个质量为m的带负电小球在平直轨道上从A点由静止开始向左运动,到达C点时小球对轨道的压力为0.已知小球运动到B点时受到的库仑力大小与小球重力大小相等,两带电小球均可看成点电荷(重力加速度g已知).求:
(1)小球在C点受到的库仑力的大小和方向;
(2)小球到达C点时的速度大小;
(3)小球从A运动至C的过程中库仑力做的功.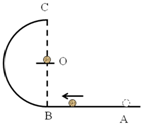
4、选择题 如图所示,长为L的长木板水平放置,在木板的A端放置一个质量为m的小物块,现缓慢地抬高A端,使木板以左端为轴转动,当木板转到与水平面的夹角为α时小物块开始滑动,此时停止转动木板,小物块滑到底端的速度为v,则在整个过程中( )
A.木板对物块做功为
| 1 2 |
| 1 2 |

5、选择题 质量m=2kg的物块放在粗糙水平面上,在水平拉力的作用下由静止开始运动,物块动能Ek与其发生位移x之间的关系如图所示.已知物块与水平面间的动摩擦因数μ=0.2,重力加速度g取10m/s2,则下列说法中正确的是( )
A.x=1m时物块的速度大小为2m/s
B.x=3m时物块的加速度大小为2.5m/s2
C.在前2m位移的运动过程中物块所经历的时间为2s
D.在前4m位移的运动过程中拉力对物块做的功为9J