时间:2019-03-16 02:55:23
1、选择题 光子的能量为hv，动量的大小为
| hv c |
| hv c2 |
| hv c2 |
参考答案：由动量守恒知，衰变后的原子核沿着与光子运动方向相反的方向运动，故A正确B错误；
hvC2仅仅是光子对应的质量亏损，而原子核具有动能，还对应部分质量亏损，故C正确D错误．
故选：AC
本题解析：
本题难度：简单
2、简答题 如图，半径为R，光滑的
| 1 4 |
参考答案：（1）物块a由M到N过程中，由机械能守恒有：mgr=12mv21 ①
由牛顿第二定律有：F-mg=mv21R ②
联立①②解得：轨道对a支持力 F=3mg
（2）物块a从N滑至D过程中，由动能定理有：-μ1mgl=12mv2D1-12mv21 ③
物块a、b在D点碰撞，根据动量守恒有：mvD1=3mvD2 ④
解得两物块在D点向左运动的速度 vD2=
本题解析：
本题难度：一般
3、简答题 如图所示，光滑水平面上有质量均为2m的小滑块A、B，A静止，B以速度
| v0 6 |
参考答案：以木块A和子弹为研究对象，规定向右为正方向，子弹射出木块的过程中根据动量守恒得：
mυ0=2mvA+mv
以木块A、B和子弹为研究对象，A、B最终以相同的速度向右运动．整个过程中根据动量守恒得：
mυ0-2mv06=5mvA
两式联立解得：v=1115υ0
答：子弹穿出A时的速度是1115υ0
本题解析：
本题难度：一般
4、选择题 如图甲所示，一质量为M的木板静止在光滑的水平地面上，现有一质量为m的小滑块以一定的初速度v0从木板的左端开始向木板的右端滑行，滑块和木板的水平速度大小随时间变化的情况如图乙所示，根据图像做出如下判断
A．滑块始终与木块存在相对运动
B．滑块未能滑出木板
C．滑块的质量m大于木板的质量
D．在t1时刻滑块从木板上滑出
参考答案：A C D
本题解析：从图中我们可以得出，最终滑块和木板做匀速直线运动
并且滑块的速度要大于木板的速度，所以两者并不是叠加在一块运动，即滑块滑出了木板。所以B错误。从t1时刻两者开始做匀速直线运动，即从这一时刻开始两者之间不在存在相互作用，所以，滑块在
时刻从木板上滑下来，所以D正确。从木板上滑下来之后，滑块以较大的速度在前做匀速直线运动，木板在后以较小的速度做匀速直线运动，所以两者始终存在相对运动。故A正确。有动量守恒公式可得
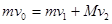（m，M分别为滑块，木板的质量，
?
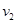分别为滑块，木板匀速运动的速度，且
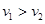）即
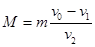，由于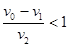
所以滑块的质量m大于木板的质量，故D正确。
本题难度：简单
5、选择题 .质量M="100" kg的小船静止在水面上,船首站着质量m甲="40" kg的游泳者甲,船尾站着质量m乙="60" kg的游泳者乙,船首指向左方.若甲、乙两游泳者同时在同一水平线上甲朝左、乙朝右以3 m/s的速率跃入水中,则( )
A．小船向左运动,速率为1 m/s
B．小船向左运动,速率为0.6 m/s
C．小船向右运动,速率大于1 m/s
D．小船仍静止
参考答案：B
本题解析：选向左的方向为正方向,由动量守恒定律得m甲v－m乙v+Mv′=0
可得船的速度为
船的速度方向向左.故选项B正确.
本题难度：简单