时间:2019-03-16 02:41:19
1、计算题 （18分）扭摆器是同步辐射装置中的插入件，能使粒子的运动轨迹发生扭摆，其简化模型如图所示：Ⅰ、Ⅱ两处宽度均为L的条形匀强磁场区边界竖直，Ⅰ区域磁场垂直纸面向外，Ⅱ区域磁场垂直纸面向里，磁感应强度大小均为B，两磁场区的间距可以调节。以Ⅰ区域左边界上的O点为坐标原点建立坐标系，y轴与左边界重合，x轴与磁场边界的交点分别为O1、O2和O3。一质量为m、电荷量为q的带正电的粒子，平行纸面从O点与y轴的夹角θ＝30°射入Ⅰ区域，粒子重力不计。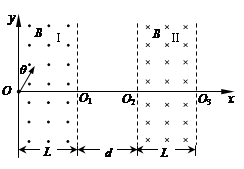
（1）若粒子恰好从O1射出Ⅰ区域，粒子的速度应为多大？
（2）若粒子从Ⅰ区域右边界射出时速度与x轴的夹角为30°，调节两磁场区的间距，粒子恰好从O3射出Ⅱ区域，则粒子从O射入到从O3射出共经历了多长时间？
参考答案：（1）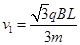
?（2）
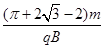
本题解析：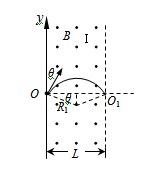
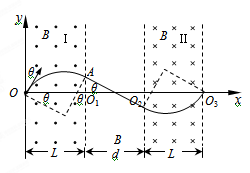（1）粒子从O1射出Ⅰ区域，轨迹如图
由几何关系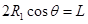
粒子在磁场中运动半径公式为：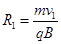
综合上式可得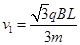
（2）粒子运动轨迹如图所示
设粒子运动速度为v2，半径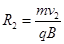
粒子在磁场中的运动周期为：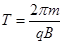
由几何关系可得，粒子在Ⅰ区域运动的圆心角为90°
即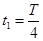
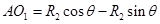
由于粒子在Ⅰ、Ⅱ区域运动半径相同，要使粒子从O3射出Ⅱ区域，则粒子在Ⅱ区域中运动时间与Ⅰ
区域相同，且粒子必须经过O1、O2的中点B，则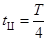
在Ⅰ、Ⅱ间隔区域运动时间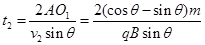
综上所述，粒子从相同O射入到O3射出共经历时间为：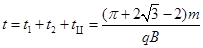
本题难度：一般
2、计算题 在光滑绝缘的水平面上建有如图所示的平面直角坐标系。空间存在着范围足够大方向竖直向上的匀强磁场。在此水平面上有均可视为质点的不带电小球a和带正电的小球b。现给a球以某一速度使其沿x轴正方向运动，当a球通过坐标系原点O瞬间，同时使b球从坐标原点O沿y轴正向以速度v0使其在磁场中做匀速圆周运动，最终b球能与a球相遇（a、b小球彼此不接触，且小球b在 运动过程中电荷量保持不变）。求：满足上述条件a球速度的大小。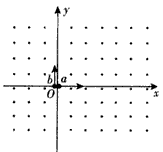
参考答案：解：b球在磁场中做匀速圆周运动
所以有
，得
周期
b球只能与a球相遇在图中的S处，相遇所需时间为
a球通过的路程为OS=2R
所以可得a球的速度大小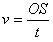
故
本题解析：
本题难度：困难
3、计算题 如图所示, 正离子束以一定的速度从a点沿ad方向射入虚线所画的正方形区域。如果在该区域中加沿ab方向的匀强电场E, 离子束刚好从c点射出。如撤出电场加一匀强磁场B, B的方向垂直纸面向外, 离子束也刚好从c点垂直bc射出。求离子束原来的速度？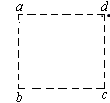
参考答案：
本题解析：设带电粒子的电量为q，质量为m，盒子的边长为L，粒子在电场中沿ab方向的位移为L，沿ad方向的位移也为L，在电场中离子做类平抛运动，设从离子从孔c射出时的速度为v，则：
，L=v0t，得：
带电粒子在磁场中做匀速圆周运动，设轨道半径为R，根据牛顿第二定律得：
，解出：
所以解得：
考点：带电粒子在电场中的运动；带电粒子在磁场中的运动。
本题难度：一般
4、填空题 质子（
参考答案：粒子在加速电场中：由动能定理得
? Ek=qU，则得 Ek1：Ek2=e：2e=1：2
粒子进入磁场后，轨道半径为 r=mvqB=
本题解析：
本题难度：一般
5、选择题 匀强磁场中的一个带电粒子，仅在磁场力作用下做匀速圆周运动。将该粒子的运动等效为环形电流，那么此电流值 （ ）
A 与粒子电荷量成正比 B 与粒子速率成正比
C与粒子质量成正比 D与磁感应强度成正比
参考答案：D
本题解析：解答本题的关键是抓住周期与B、I的联系． 设带电粒子以速率v垂直射入磁感强度为B的匀强磁场中，带电粒子在匀强磁场中做匀速圆周运动的周期为T，半径为r，由洛伦兹力提供向心力，根据牛顿第二定律得
，于是有 
，由电流的定义式得环形电流：
，由此可见，I与q的平方成正比，与v无关，与B成正比，与m成反比，故选D．
考点：本题是洛伦兹力、向心力和电流等知识的综合应用，主要考查电流概念、牛顿第二定律、向心力、带电粒子在匀强磁场中的运动等知识点．
本题难度：一般