时间:2019-03-16 01:52:00
1、计算题 如图所示，光滑水平面右端B处连接一个竖直的半径为R的光滑半圆轨道，在离B距离为L的A点，用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力，质点沿半圆轨道运动到C处后恰好落到A点，求：
（1）推力对小球做了多少功？（用题中所给的量表示）
（2）L取何值时，完成上述运动所做的功最少？最小功为多少？
（3）L取何值时，完成上述运动所用的力最小？最小力为多少？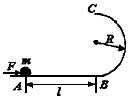 
参考答案：（1）WF=2mgR+
（2）l=2R时，WFm=5mgR/2
（3）l=4R时，Fm=mg
本题解析：
本题难度：困难
2、计算题 如图所示，小球由静止开始沿光滑轨道滑下，接着水平抛出。小球抛出后落在斜面上。已知斜面的倾角为θ，斜面底端在抛出点正下方，斜面顶端与抛出点在同一水平面上，斜面长度为L，斜面上M、N两点将斜面长度等分为3段，小球可以看作质点，空气阻力不计。为使小球能落在M点以上，小球开始时释放的位置相对于抛出点的高度h应满足什么条件？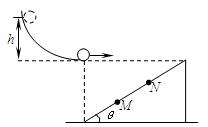
参考答案：小球沿轨道滑下，由动能定理得：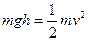
?…………………………4分
小球离开桌面后做平抛运动： x =v0t? y =gt2/2 ?…………………………2分+2分
得：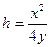 
为使小球落在M点以上，应满足：
当? y=2Lsinθ/3时? x>Lcosθ/3?…………………………2分
本题解析：故要使小球落在M点以上，则h 满足的条件：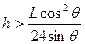
?……………………4分略
本题难度：简单
3、选择题 如图所示，质量为m的物体从半径为R的l／4圆轨道的上端由静止滑到最低点，然后又沿水平地面运动一段距离停下来，物体与圆轨道和水平面间的滑动摩擦因数均为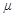
，物体全程克服摩擦力做功为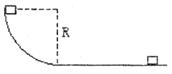
A．0
B．
C．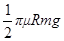
D．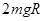
参考答案：B
本题解析：由动能定理设克服摩擦力做功为W,mgR-W=o,W=mgR，B对；
本题难度：一般
4、简答题 如多所示，一质量为m的小球，用长为L的轻绳悬挂于O点，
（1）小球在水平拉力F的作用下从平衡位置P点缓慢地移动到Q点，此时悬线与竖直方向的夹角为θ；
（2）小球在水平恒力F作用下由P点移动到Q点，此时悬线与竖直方向的夹角为θ．
求上述（1）、（2）两种情况下拉力F所做的功各为多大？
参考答案：（着）小球从平衡位置P点缓慢地移动到Q点的过程中，根据动能定理的
&dbsp;&dbsp; W着-mgL（着-cosθ）=0&dbsp;&dbsp;&dbsp;
的&dbsp;拉力F所做的功为W着=mgL（着-cosθ）
（2）水平力F为恒力时，由P点移动到Q点，拉力F所做的功为W2=FLsidθ．
答：（着）小球在水平拉力F的作用下从平衡位置P点缓慢地移动到Q点，拉力F所做的功为mgL（着-cosθ）．
（2）小球在水平恒力F作用下由P点移动到Q点，拉力F所做的功为FLsidθ．
本题解析：
本题难度：一般
5、简答题 质量均为m的物体A和B分别系在一根不计质量的细绳两端，绳子跨过固定在倾角为30°的斜面顶端的定滑轮上，斜面固定在水平地面上，开始时把物体B拉到斜面底端，这时物体A离地面的高度为0.8m，如图所示．．若摩擦力均不计，从静止开始放手让它们运动．（斜面足够长，g取10m/s2）求：
（1）物体A着地时的速度；
（2）物体B能沿斜面滑行的最大距离是多少？
参考答案：（1）、设A落地时的速度为v，系统的机械能守恒：
? mgh-mghsinα=12(m+m)v2，
? 代入数据得：V=2?m/s．
?（2）、A落地后，B以v为初速度沿斜面匀减速上升，设沿斜面又上升的距离为S，
? 由动能定理得：-mgSsinα=0-12mv2
? ? 物体m能沿斜面滑行的最大距离：L=h+S?
? 代入数据得：L=1.2m
答：（1）、物体A着地时的速度是2m/s．
? （2）、物体B能沿斜面滑行的最大距离是1.2m．
本题解析：
本题难度：一般