时间:2019-03-16 01:52:00
1、计算题 如图甲所示,水平加速电场的加速电压为U0,在它的右侧有由水平正对放置的平行金属板a、b构成的偏转电场,已知偏转电场的板长L="0.10" m,板间距离d=5.0×10-2m,两板间接有如图15乙所示的随时间变化的电压U,且a板电势高于b板电势。在金属板右侧存在有界的匀强磁场,磁场的左边界为与金属板右侧重合的竖直平面MN,MN右侧的磁场范围足够大,磁感应强度B=5.0×10-3T,方向与偏转电场正交向里(垂直纸面向里)。质量和电荷量都相同的带正电的粒子从静止开始经过电压U0=50V的加速电场后,连续沿两金属板间的中线OO′方向射入偏转电场中,中线OO′与磁场边界MN垂直。已知带电粒子的比荷 =1.0×108C/kg,不计粒子所受的重力和粒子间的相互作用力,忽略偏转电场两板间电场的边缘效应,在每个粒子通过偏转电场区域的极短时间内,偏转电场可视作恒定不变。
=1.0×108C/kg,不计粒子所受的重力和粒子间的相互作用力,忽略偏转电场两板间电场的边缘效应,在每个粒子通过偏转电场区域的极短时间内,偏转电场可视作恒定不变。
(1)求t=0时刻射入偏转电场的粒子在磁场边界上的入射点和出射点间的距离;
(2)求粒子进入磁场时的最大速度;
(3)对于所有进入磁场中的粒子,如果要增大粒子在磁场边界上的入射点和出射点间的距离,应该采取哪些措施?试从理论上推理说明。
参考答案:
(1)0.40m(2)1.1×105m/s(3)要增大粒子在磁场边界上的入射点和出射点间的距离x,应该减小匀强磁场的磁感应强度B,或增大加速电压U0
本题解析:
(1)设经过加速电场加速后,粒子的速度为v0,根据动能定理有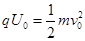 ,解得
,解得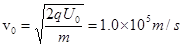 .由于t=0时刻偏转电场的场强为零,所以此时射入偏转电场的粒子将匀速穿过电场而以v0的速度垂直磁场边界进入磁场中,在磁场中的运动轨迹为半圆。
.由于t=0时刻偏转电场的场强为零,所以此时射入偏转电场的粒子将匀速穿过电场而以v0的速度垂直磁场边界进入磁场中,在磁场中的运动轨迹为半圆。
设粒子在磁场中做匀速圆周运动的半径为r,由洛仑兹力公式和牛顿第二定律得?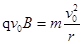 解得
解得 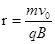 ?所以粒子在磁场边界上的入射点和出射点间的距离d=2r=0.40m
?所以粒子在磁场边界上的入射点和出射点间的距离d=2r=0.40m
(2)设粒子以最大偏转量离开偏转电场,即轨迹经过金属板右侧边缘处,进入磁场时a、b板的电压为Um,则粒子进入偏转电场后,加速度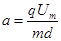
水平方向 L=v0t
竖直方向 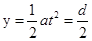
解得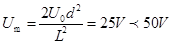
所以,电压Um=25V时对应粒子进入磁场的速度最大,设最大速度大小为vm,方向与OO′的夹角为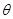 ,则对于粒子通过加速电场和偏转电场的过程,根据动能定理有:
,则对于粒子通过加速电场和偏转电场的过程,根据动能定理有: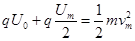
解得 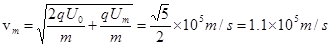
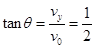 ,即?
,即? (或
(或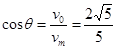 ,即
,即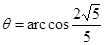 )
)
(说明:计算结果带有根号,结果正确的同样得分)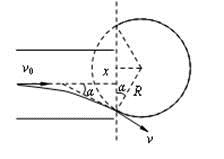
(3)设任意时刻进入磁场的粒子,其进入磁场时速度方向与OO′的夹角为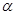 ,则其速度大小
,则其速度大小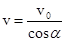
粒子在磁场中做圆周运动的轨迹半径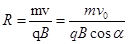 ?
?
由如图所示的几何关系可知,粒子在磁场边界上的入射点和出射点间的距离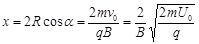
所以要增大粒子在磁场边界上的入射点和出射点间的距离x,应该减小匀强磁场的磁感应强度B,或增大加速电压U0
本题难度:一般
2、计算题 (2012年2月重庆八中检测)如图所示,可视为质点的总质量(包括装备)为m=60kg的滑板运动员,从高为H=15m的斜面AB的顶端A点由静止开始沿斜面下滑,在 点进入光滑的四分之一圆弧BC,圆弧BC半径为R=5m,运动员经C点沿竖直轨道冲出向上运动,经时间t=2s后又落回轨道。若运动员经C点后在空中运动时只受重力,轨道AB段粗糙、BC段光滑。g=10m/s2。
点进入光滑的四分之一圆弧BC,圆弧BC半径为R=5m,运动员经C点沿竖直轨道冲出向上运动,经时间t=2s后又落回轨道。若运动员经C点后在空中运动时只受重力,轨道AB段粗糙、BC段光滑。g=10m/s2。
求:(1)运动员在C点的速度和离开C点可上升的高度。
(2)运动员(包括装备)运动到圆轨道最低点B时对轨道的压力大小。
(3)从A点到B点,运动员损失的机械能。
参考答案:(1)5m(2)3000N(3)3000J
本题解析:(1)运动员在C点的速度 =10m/s,
=10m/s,
离开C点可上升的高度h=
 ?=5m。
?=5m。
(2)设运动员运动到圆轨道最低点B时速度为v2,对运动员从 到
到 :
: ?(2分)
?(2分)
在最低点B,由牛顿第二定律,F-mg=m ,
,
解得:F=3000N。
由牛顿第三定律,运动员对轨道的压力大小F’=F=3000N。
(3)从A点到B点,由能量守恒定律,运动员损失的机械能:
△E= =3000J。
=3000J。
本题难度:一般
3、选择题 (选考题)如图所示,一个长为L,质量为M的长方形木板,静止在光滑水平面上,一个质量为m的物块(可视为质点),以水平初速度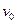 ,从木板的左端滑向另一端,设物块与木板间的动摩擦因数为
,从木板的左端滑向另一端,设物块与木板间的动摩擦因数为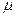 ,当物块与木板达到相对静止时,物块仍在长木板上,物块相对木板的位移为d,木板相对地面的位移为s。则在此过程中
,当物块与木板达到相对静止时,物块仍在长木板上,物块相对木板的位移为d,木板相对地面的位移为s。则在此过程中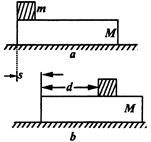
A.摩擦力对木板做功为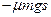
B.摩擦力对物块做功为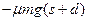
C.木板动能的增量为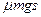
D.系统由于摩擦而产生的热量为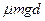
参考答案:BCD
本题解析:略
本题难度:简单
4、简答题 如图所示,一水平方向的传送带以恒定速度v=2m/s沿顺时针方向匀速转动,传送带右端固定着一光滑的四分之一圆弧轨道,并与弧下端相切.一质量m=1kg的物体自圆弧轨道的最高点由静止滑下,圆弧轨道的半径尺R=0.45m,物体与传送带之间的动摩擦因数μ=0.2,不计物体滑过曲面与传送带交接处时的能量损失,传送带足够长,取g=10m/s2.
(1)求物体从第一次滑上传送带到离开传送带所经历的时间;
(2)求物体从第一次滑上传送带到离开传送带的过程中,传送带对物体做的功及由于摩擦产生的热量;
(3)求物体从第二次滑上传送带到离开传送带的过程中,传送带对物体做的功及由于摩擦产生的热量;
(4)经过足够长的时间之后物体能否停下来?若能,请说明物体停下的位置;若不能,请简述物体的运动规律.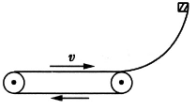
参考答案:(1)物体沿圆弧轨道下滑的过程中机械能守恒,设物体滑到传送带右端时的速度为v1,则有:
mgR=12mv12.
解得v1=3m/s.
物体在传送带上运动的加速度大小为a=μmgm=μg=2m/s2.
物体在传送带上向左运动的时间t1=v1a=1.5s.
向左运动的最大距离s=v122a=2.25m.
物体向右运动达到速度为v时,向右运动的距离s1=v22a=1m.
所用的时间t2=va=1s,匀速运动的时间t3=s-s1v=0.625s.
所以t=t1+t2+t3=1.5+1+0.625s=3.125s.
(2)根据动能定理得,传送带对物体做的功
W=12mv2-12mv12=-2.5J.
物体相对传送带滑过的路程△x=v2-v12-2a+v(t1+t2)=6.25m
由于摩擦产生的热量Q=μmg?△x=12.5J.
(3)根据机械能守恒定律,物体第二次滑上传送带时的速度为2m/s.
物体先向左做匀减速运动,减速到速度为零,然后向右做匀加速运动,直到速度变为v=2m/s.
时间t4=2va=2s.
根据动能定理,由于物体从滑上传送带到离开传送带过程中物体的动能没有变化,故传送带对物体所做的功W2=0.
在这段时间内物体相对传送带滑过的路程△x2=vt4=4m
所以由于摩擦产生的热量为
Q′=μmg?△x2=0.2×1×10×4J=8J.
(4)物体不会停下来,物体在圆弧轨道和传送带上做周期性往复运动.
本题解析:
本题难度:一般
5、计算题 (16分)如图所示,水平地面上固定有高为h的平台,台面上有固定的光滑坡道,坡道顶端距台面高度也为h,坡道底端与台面相切。小球A从坡道顶端由静止开始滑下,到达水平光滑的台面与静止在台面上的小球B发生碰撞,并粘连在一起,共同沿台面滑行并从台面边缘飞出,落地点与飞出点的水平距离恰好为台高的一半,两球均可视为质点,忽略空气阻力,重力加速度为g。求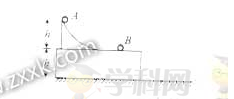
(1)小球A刚滑至水平台面的速度vA;
(2)A、B两球的质量之比mA:mB。
参考答案:(1)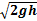 (2)1:3
(2)1:3
本题解析:解:(1)小球从坡道顶端滑至水平台面的过程中,由机械能守恒定律得
mAgh =  mAvA2
mAvA2
解得:vA = 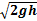
(2)设两球碰撞后共同的速度为v,由动量守恒定律得
mAvA=(mA + m?B)v
粘在一起的两球飞出台面后做平抛运动
竖直方向:h =  gt2
gt2
水平方向: ?= vt
?= vt
联立上式各式解得: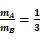
本题难度:简单