时间:2019-03-15 18:19:13
1、选择题 以加速度a=0.5m/s2做匀变速直线运动的质点，在它任何1s时间内的（ ）
A．末速度是初速度的0.5倍
B．位移是0.5m
C．速度的变化量是0.5m/s
D．平均速度是0.5m/s
参考答案：
A、C、根据△v=at=0.5×1m/s=0.5m/s，则知任何1s时间内的速度的变化量为2m/s，1s内的末速度比初速度大2m/s，但末速度不一定是初速度的0.5倍．故A错误，C正确；
B、D、根据位移时间公式x=v0t+12at2，可知因为初速度未知，故无法求出任意1s内的位移，也无法求出任意1s内的平均速度．故B、D错误；
故选：C．
本题解析：
本题难度：一般
2、计算题 （10分）如图所示，A、B两棒的长均为L="1" m，A的下端和B的上端相距s="20" m．若A、B同时运动，A做自由落体运动，B做竖直上抛运动，初速度
="40" m/s．求：（g取10 m/s。）
（1）A、B两棒何时相遇．
（2）A、B两棒从相遇开始到分离所需的时间．
参考答案：（1）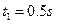
（2）
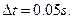
本题解析：（1）设经过时间t1两棒相遇，由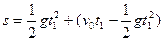
（3分）
得
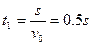（1分）
（2）设经过时间如两棒分离，由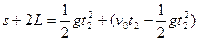
（3分）
解得：
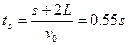（分）
所以两棒从相遇开始到分离所需的时间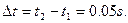
（2分）
本题难度：一般
3、计算题 （15分）一辆轿车违章超车，以108 km/h的速度驶入左侧逆行道时，猛然发现、正前方80 m处一辆卡车正以72 km/h的速度迎面驶来，两车司机同时刹车，刹车加速度大小都是10 m/s2，两司机的反应时间(即司机发现险情到实施刹车所经历的时间)都是Δt.试问Δt是何数值，才能保证两车不相撞?
参考答案：Δt＜0.3 s
本题解析：设轿车行驶的速度为v1，卡车行驶的速度为v2，则v1＝108 km/h="30" m/s，v2＝72 km/h="20" m/s，在反应时间Δt内两车行驶的距离分别为s1、s2，则
s1＝v1Δt?①?
s2＝v2Δt?②?
轿车、卡车刹车所通过的距离分别为s3、s4?则
s3＝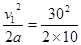
?m＝45 m?③?
s4＝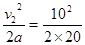
?m＝20 m④?为保证两车不相撞，必须?
s1＋s2＋s3＋s4＜80 m?⑤?
将①②③④代入⑤解得?Δt＜0.3 s
点评：本题考查了利用匀变速直线运动规律，通过解析法建立等式找出不相撞的等式关系，从而列式求出时间。这样的方法在此类为题中十分常见。
本题难度：一般
4、计算题 如图所示，一条上端固定的绳长l1=7．5m，质量m=60Kg的特技演员从绳上端先沿绳从静止开始无摩擦下滑一段距离后，突然握紧绳子，与绳子之间产生f="1800" N的摩擦阻力。滑到绳子末端时速度刚好为零。求：
（1）特技演员下滑所用的时间t．
（2）在水平面上有一辆长l2=3m平板车，其上表面与绳末端等高，车右端离绳末端s=4m，平板车能一直以v
="2" m/s的恒定速度向右运动，为了要让该演员滑下后能留在车上，则车启动后演员应在多长时间范围内开始下滑？（把人看作质点，人与车之间动摩擦系数μ=0.2， g取10m/s2）
参考答案：（1）1.5s? (2)大于0.5s小于1.5s
本题解析：（1）特技演员沿绳子下滑过程分为两个阶段，第一个阶段自由落体运动，设末速度v，则第二阶段初速度也是v
第一阶段加速度为g，下落的高度
第二阶段加速度
，下落的高度
那么
，解得v=10m/s
第一段运动时间
第二段运动时间
所以下滑所用时间
（2）人落在车上没有速度，而车以2m/s匀速运动，人做匀加速运动，加速度
，当人加速到2m/s时与车一起匀速，那么匀加速的时间
，此过程，小车位移
人的位移
，即人在车上相对滑动距离为
，所以人滑到车上时与车左端相距大于等于1m。即车移动的距离小于
，但是要让人落在车上，车的位移还要大于
，
车的位移小于6m大于4m，车的运动时间
，即
，而演员下滑需要1.5s
所以车启动后演员要在
时间内开始下滑，
所以车启动后演员要在0.5s到1.5s时间内开始下滑。
本题难度：一般
5、计算题 （5分）根据匀变速直线运动速度公式和位移公式推证：匀变速直线运动的速度和位移关系是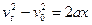
参考答案：
本题解析：略
本题难度：一般