时间:2019-03-15 17:47:45
1、实验题 如图6-8所示，用长为L且不可伸长的细线连结质量为m的小球，绳的O端固定，另用细线AB将小球拉起使之与水平方向成30°角.现将AB线从A处剪断，则剪断细线AB的瞬间小球的加速度大小为____________，方向____________，剪断细线AB后小球落到最低点时细线L中的张力为____________.
图6-8
参考答案：g?竖直向下? 1.5mg
本题解析：AB剪断后球先自由落体至绳子绷紧后摆动，故球的瞬间加速度为g.自由落体的末速度v1=
摆动到最低点,根据动能定理mgL(1-cos60°)=
mv22-m(v1cos30°)2
T-mg=mv22/L，T=1.5mg.
本题难度：简单
2、填空题 木块受水平力F作用在水平面上由静止开始运动，前进s后撤去F，木块又沿原方向前进3s停止，则摩擦力f=________，木块最大动能为________。
参考答案：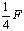
，
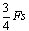
本题解析：
本题难度：一般
3、计算题 如图所示，光滑水平轨道与半径为R的光滑竖直半圆轨道在B点平滑连接。在过圆心O的水平界面MN的下方分布有水平向右的匀强电场。现有一质量为m，电量为+q的小球从水平轨道上A点由静止释放，小球运动到C点离开圆轨道后，经界面MN上的P点进入电场（P点恰好在A点的正上方，如图。小球可视为质点，小球运动到C点之前电量保持不变，经过C点后电量立即变为零）。已知A、B间距离为2R，重力加速度为g。在上述运动过程中，求：
（1）电场强度E的大小；
（2）小球在圆轨道上运动时最大速率；
（3）小球对圆轨道的最大压力的大小。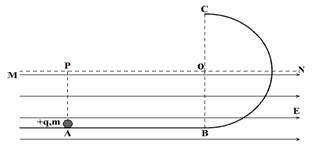 
参考答案：解：（1）设电场强度为E，小球过C点时速度大小为
，小球从A到C由动能定理：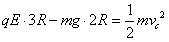 
小球离开C点后做平抛运动到P点：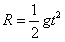 
，
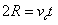
联立方程解得：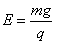
（2）设小球运动到圆周D点时速度最大为v，此时OD与竖直线OB夹角设为α，小球从A运动到D过程，根据动能定理：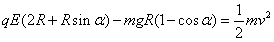
即：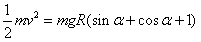
根据数学知识可得，当α=45°时动能最大
由此可得：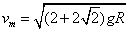
（3）由于小球在D点时速度最大且电场力与重力的合力恰好沿半径方向，故小球在的点对圆轨道的压力最大，设此压力大小为F，由牛顿第三定律可知小球在D点受到的轨道弹力大小也为F，在D点对小球进行受力分析，并建立如图所示坐标系，由牛顿第二定律：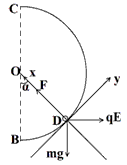 
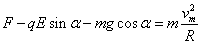
解得：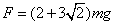
本题解析：
本题难度：困难
4、选择题 一个质量为m的物体，从静止开始以
| g 3 |
| mgh 3 |
| mgh 3 |
| mgh 3 |
参考答案：物体所受的合力为F合=ma=13mg，则合力功为W合=13mgh，所以动能增加了13mgh．重力做正功，重力势能减小mgh，则机械能减小23mgh．故A、B、D正确，C错误．
故选ABD．
本题解析：
本题难度：一般
5、选择题 人从高h处将一质量为m的小球水平抛出，不计空气阻力，测得球落地时速度大小为υ，则人抛球时对小球做的功为（ ）
A．mgh-
| 1 2 |
| 1 2 |
| 1 2 |
| 1 2 |
参考答案：对小球，从抛出到落地的整个过程中，由动能定理得：W+mgh=12mv2，
解得人对小球做功：W=12mv2-mgh；
故选：C．
本题解析：
本题难度：简单