时间:2019-03-15 17:37:22
1、选择题 如图所示，在高1.5 m的光滑平台上有一个质量为2 kg的小球被一细线拴在墙上，球与墙之间有一根被压缩的轻质弹簧．当烧断细线时，小球被弹出，小球落地时的速度方向与水平方向成60°角，则弹簧被压缩时具有的弹性势能为(g＝10 m/s2) ( )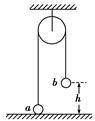
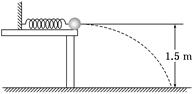
图2
A．10 J
B．15 J
C．20 J
D．25 J
2、计算题 如图所示，高Ｈ＝1.6m的赛台ABCDE固定于地面上，其上表面ABC光滑；质量Ｍ＝1kg、高h＝0.8m、长Ｌ的小车Q紧靠赛台右侧CD面（不粘连），放置于光滑水平地面上．质量m ＝1kg的小物块P从赛台顶点Ａ由静止释放，经过Ｂ点的小曲面无损失机械能的滑上BC水平面，再滑上小车的左端．已知小物块与小车上表面的动摩擦因数μ＝0.4，g取10m/s2．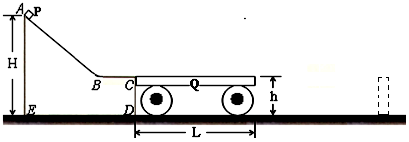
（1）求小物块P滑上小车左端时的速度v１。
（2）如果小物块没有从小车上滑脱，求小车最短长度Ｌ0 。
（3）若小车长Ｌ＝1.2m，距离小车右端S处有与车面等高的竖直挡板，小车碰上挡板后立即停止不动，讨论小物块在小车上运动过程中，克服摩擦力做功Wf与S的关系。
3、计算题 （19分）如图所示，半径为R的四分之一圆弧形支架竖直放置，圆弧边缘C处有一小定滑轮，绳子不可伸长，不计一切摩擦，开始时，m1、m2两球静止，且m1＞m2，试求：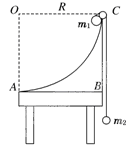
(1)m1释放后沿圆弧滑至最低点A时的速度．
(2)若A点离地高度为2R，m1滑到A点时绳子突然断开，则m1落地点离A点的水平距离是多少？
(3)为使m1能到达A点，m1与m2之间必须满足什么关系．
4、计算题 （原创）（16分）某兴趣小组设计了一种实验装置，用来研究碰撞问题，其模型如图所示，光滑轨道中间部分水平，右侧为位于竖直平面内半径为R的半圆，在最低点与直轨道相切．5个大小相同、质量不等的小球并列静置于水平部分，球间有微小间隔，从左到右，球的编号依次为0、1、2、3、4，球的质量依次递减，每球质量与其相邻左球质量之比为k（k<1）.将0号球向左拉至左侧轨道距水平高h处，然后由静止释放，使其与1号球碰撞，1号球再与2号球碰撞……所有碰撞皆为无机械能损失的正碰（不计空气阻力，小球可视为质点，重力加速度为g）.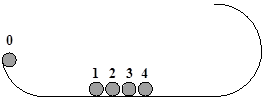
（1）0号球与1号球碰撞后，1号球的速度大小v1；
（2）若已知h=0.1m，R=0.64m，要使4号球碰撞后能过右侧轨道的最高点，问k值为多少？
5、选择题 由光滑细管组成的轨道如图所示，其中AB段和BC段是半径为R的四分之一圆弧，轨道固定在竖直平面内。一质量为m的小球，从距离水平地面为H的管口D处静止释放，最后能够从A端水平抛出落到地面上。下列说法正确的是（ ）
A．小球能从细管A端水平抛出的条件是H>2R
B．小球到达A点时对细管的作用力一定随H的增大而增大
C．小球落地相对于A点的水平位移大小为
D．若H不变，则当
时，小球落地相对于A点的水平距离最大，且最大为H