时间:2018-10-13 01:17:59
1、选择题 如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
A.球A的线速度一定大于球B的线速度?
B.球A的角速度一定小于球B的角速度?
C.球A的运动周期一定小于球B的运动周期?
D.球A对筒壁的压力一定大于球B对筒壁的压力?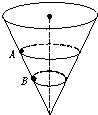
参考答案:A、对小球受力分析,受重力和支持力,如图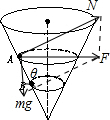
根据牛顿第二定律,有
F=mgtanθ=mv2r
解得
v=
本题解析:
本题难度:一般
2、简答题 “和平号”空间站已于今年3月23日成功地坠落在太平洋海域,坠落过程可简化为从一个近圆轨道(可近似看作圆轨道)开始,经过与大气摩擦,空间站的绝大部分经过升温、熔化,最后汽化面销毁,剩下的残片坠入大海.此过程中,空间站原来的机械能中,除一部分用于销毁和一部分被残片带走外,还有一部分能量E′通过其他方式散失(不考虑坠落过程中化学反应的能量)
(1)试导出以下各物理量的符号表示散失能量E′的公式.(2)算出E′的数值.(结果保留两位有效数字)
坠落开始时空间站的质量M=1.17×105Kg;
轨道离地的高度为h=146Km地球半径R=6.4×106m;
坠落窨范围内重力加速度可看作g=10m/s2;
入海残片的质量m=1.2×104Kg;
入海残片的温升高△T=3000K;
入海残片的入海速度为声速v=340m/s;
空间站材料每1千克升温1K平均所需能量C=1.0×103J;
每销毁1千克材料平均所需能量μ=1.0×107J.
参考答案:(1)根据题给条件,从近圆轨道到地面的空间中重力加速度g=10m/s2,.若以地面为重力势能零点,坠落过程开始时空间站在近圆轨道的势能为:
EP=Mgh?①
以v表示空间站在近圆轨道上的速度,有牛顿第二定律得:
Mg=?Mv2r? ②
其中r为轨道半径,若以R地表示地球半径,则:
r=R地+h? ③
由②③可得空间站在近圆轨道上的动能为:
EK=12Mg(R地+h)? ④
由①④可得,在近圆轨道上的机械能为:
?E=Mg(12R地+32h)? ⑤
在坠落过程中,用于销毁部分所需能量为:
Q汽=(M-m)μ? ⑥
用于残片升温所需能量:
Q残=cm△T? ⑦
残片的动能:
E残=12mv2? ⑧
以E′表示其他方式散失的能量,则有能量守恒得:
E=Q汽+E残+Q残+E/? ⑨
故散失能量E′的公式为:E/=Mg(12R地+32h)?-(M-m)μ-12mv2-cm△T.
(2)以题给数据代入得:
E′=2.9×1012J
故E′的数值为:E′=2.9×1012J.
本题解析:
本题难度:一般
3、选择题 如图,M为固定在桌面上的L形木块,abcd为3/4圆周的光滑轨道,a为轨道的最高点,de面水平且有一定长度.今将质量为m的小球在d点的正上方高h处释放,让其自由下落到d处切入轨道运动,则( )
A.在h一定的条件下,释放后小球的运动情况与小球的质量有关
B.只要改变h的大小,就能使小球通过a点之后,既可能落回轨道之内,又可能落到de面上
C.无论怎样改变h的大小,都不可能使小球通过a点之后,又落回轨道之内
D.要使小球飞出de面之外(即e的右面)是可能的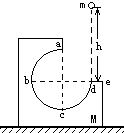
参考答案:A、释放后小球只受重力,根据动能定理得:
mgh=12mv2,
v=
本题解析:
本题难度:一般
4、简答题 如图所示,在匀速转动的圆盘上,沿直径方向上放置以细线相连的A、B两个小物块.A的质量为mA=2kg,离轴心r1=20cm,B的质量为mB=1kg,离轴心r2=10cm,A、B与盘面间相互作用的摩擦力最大值为其重力的0.5倍,试求:
(1)当圆盘转动的角速度ω0为多少时,细线上开始出现张力?
(2)欲使A、B与盘面间不发生相对滑动,则圆盘转动的最大角速度为多大?(g=10m/s2)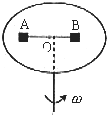
参考答案:(1)ω较小时,A、B均由静摩擦力充当向心力,ω增大,F=mω2r可知,它们受到的静摩擦力也增大,而r1>r2,所以A受到的静摩擦力先达到最大值.ω再增大,AB间绳子开始受到拉力.
由Ffm=mAω20r0,得:ω0=
本题解析:
本题难度:一般
5、计算题 质量相等的小球A、B分别固定在轻杆的中点及端点,当棒在光滑的水平面上绕O点匀速转动时,如图。求棒的OA段及AB段对球的拉力之比。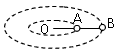
参考答案:解:设OA、AB段拉力分别为F1、F2,长度分别为r和2r,则有:
? F1-F2 = mω2r ……(1)
? F2=mω22 r …… (2)
? 由(1)(2)可得: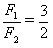
本题解析:
本题难度:困难