时间:2018-10-13 01:16:28
1、简答题 如图所示,空间分布着有理想边界的匀强电场和匀强磁场.左侧匀强电场的场强大小为E、方向水平向右,电场宽度为L;中间区域及右侧匀强磁场的磁感应强度大小均为B,方向垂直纸面向外和向里.一个质量为m、电量为q、不计重力的带正电的粒子从电场的左边缘的O点由静止开始运动,穿过中间磁场区域进入右侧磁场区域后,又回到O点,然后重复上述运动过程.要求:
(1)定性画出粒子运动轨迹,并求出粒子在磁场中运动的轨道半径R;
(2)中间磁场区域的宽度d;
(3)带电粒子从O点开始运动到第一次回到O点所用时间t.
参考答案:
(1)粒子运动轨迹如图所示;
带电粒子在电场中加速,qEL=12mv2
带电粒子在磁场中偏转,Bqv=mv2R?可得?R=1B
本题解析:
本题难度:一般
2、选择题 如图所示,小物块放在水平转盘上,随盘同步做匀速圆周运动,则下列关于物块受力情况的叙述中正确的是( )
A.受重力、支持力、静摩擦力和向心力的作用
B.摩擦力的方向始终指向圆心O
C.摩擦力的方向始终与线速度的方向相同
D.静摩擦力提供使物体做匀速圆周运动的向心力
参考答案:A、小物块受到重力、支持力和静摩擦力三个力,向心力是物体做圆周运动所需要的力.故A错误.
? B、物块做圆周运动所需要的向心力由静摩擦力提供,向心力的方向指向圆心,所以静摩擦力的方向指向圆心.故B、D正确,C错误.
故选BD.
本题解析:
本题难度:简单
3、填空题 一段长为L的导线弯成3/4圆周形状,置于垂直于纸面向外的匀强磁场中,磁感强度为B.如图示.若此导线以速度v沿纸面向上运动,则导线两端点a、d间的电势差Uad=______.若导线绕过a点与磁场方向平行的轴以角速度ω顺时针转动时,a、d两点间的电势差Uad=______.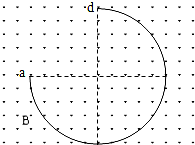
参考答案:导线长为L,圆的半径为R=2L3π,当以速度v沿纸面向上运动,34圆周的右半部分,相当于没有感应电动势,而左半部分的有效切割长度为圆的半径,则导线产生的感应电动势E=BRV=2BLv3π,根据右手定则可知,若是闭合电路,则感应电流的方向a→d,由于是电源内部,所以a点的电势低于d电势,
则Uad=-2BLv3π;
同理:当导线绕过a点与磁场方向平行的轴以角速度ω顺时针转动时,有效切割长度为半径的
本题解析:
本题难度:简单
4、简答题 如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B.现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出,最终打到Q点,不计微粒的重力.求:
(1)微粒在磁场中运动的周期;
(2)从P点到Q点,微粒的运动速度大小及运动时间;
(3)若向里磁场是有界的,分布在以O点为圆心、半径为R和2R的两半圆之间的区域,上述微粒仍从P点沿半径方向向左侧射出,且微粒仍能到达Q点,求其速度的最大值.
参考答案:(1)由qvB=mv2r及T=2πrv得:
微粒在磁场中运动的周期? T=2πmqB.
(2)令n表示带电粒子在磁场中运动时的圆心个数,则
由几何关系可知,微粒运动的轨道半径r应满足:r=Rtanπ2n,(n=2,3,4,5,…),
结合(1)可知,v=qBrm=qBmRtanπ2n,(n=2,3,4,5,…);
相应的运动轨迹所对应的圆心角φ满足:
①当n为偶数时,φ=(2π-n-1nπ)?n2+n-1nπ?n2=nπ;(n=2,4,6,8,…)
②当n为奇数时,φ=(2π-n-1nπ)?n+12+n-1nπ?n-12=n2+1nπ;(n=3,5,7,9,…)
对应的运动时间t满足:
①当n为偶数时,t=n2T=nπmqB,(n=2,4,6,8,…);
②当n为奇数时,t=n2+1n?T2=(n2+1)πmnqB;(n=3,5,7,9,…)
(3)由几何关系可知,rn+rnsinπ2n≤2R,(n=2,3,4,5,…);
得:当n=3时,r可取满足条件的最大值,rmax=
本题解析:
本题难度:一般
5、选择题 如图所示为圆柱形区域的横截面,在没有磁场的情况下,带电粒子(不计重力)以某一初速度沿截面直径方向入射,穿过此区域的时间为t,在该区域加沿轴线方向的匀强磁场,磁感应强度为B,带电粒子仍以同一初速度沿截面直径入射,粒子飞出此区域时,速度方向偏转60°角,如图所示,根据上述条件可求下列物理量中的( )
A.带电粒子的比荷
B.带电粒子在磁场中运动的周期
C.带电粒子在磁场中运动的半径
D.带电粒子的初速度
参考答案:无磁场时,带电粒子做匀速直线运动,设圆柱形区域磁场的半径为R0,则v=2R0t? (1)
而有磁场时,带电粒子做匀速圆周运动,由半径公式可得:R=mvBq? (2)
由几何关系得,圆磁场半径与圆轨道半径的关系:R=
本题解析:
本题难度:简单