时间:2018-10-13 00:21:46
1、计算题 如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子。在放射源右边有一很薄的挡板,挡板与xoy平面交线的两端M、N与原点O正好构成等腰直角三角形。已知带电粒子的质量为m,带电量为+q,速度为υ,MN的长度为L。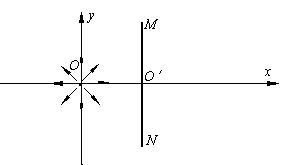
(1) 若在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧所有运动的粒子都能打到挡板MN上,则电场强度E0的最小值为多大?在电场强度为E0时,打到板上的粒子动能为多大?
若在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧所有运动的粒子都能打到挡板MN上,则电场强度E0的最小值为多大?在电场强度为E0时,打到板上的粒子动能为多大?
(2)若在整个空间加一方向垂直纸面向里的匀强磁场,要使板右侧的MN连线上都有粒子打到,磁场的磁感应强度不能超过多少(用m、υ、q、L表示)?若满足此条件,放射源O向外发射出的所有带电粒子中有几分之几能打在板的左边?
参考答案: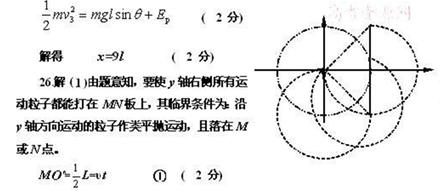

本题解析:略
本题难度:简单
2、选择题 如图所示,在虚线方框内的空间有方向竖直向下的匀强电场和垂直纸面向里的匀强磁场,一带电粒子垂直电场和磁场方向飞入场中,恰好做匀速直线运动,水平飞离正交电磁场。如果该区域只有电场,粒子将从a点飞离,穿越场区的时间为t1,飞离时速度大小为v1;如果只有磁场,粒子将从b点飞离,穿越场区的时间为t2,飞离时速度大小为v2,重力忽略不计,则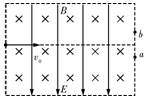
A.t1<t2
B.t1>t2
C.v1>v2
D.v1<v2
参考答案:AC
本题解析:略
本题难度:一般
3、计算题 (18分)如图所示,平行且足够长的两条光滑金属导轨,相距0.5 m,与水平面夹角为30°,不计电阻,广阔的匀强磁场垂直穿过导轨平面,磁感应强度B=0.4 T,垂直导轨放置两金属棒 和
和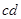 ,长度均为0.5 m,电阻均为0.1Ω,质量分别为0.1 kg和0.2 kg,两金属棒与金属导轨接触良好且可沿导轨自由滑动。现
,长度均为0.5 m,电阻均为0.1Ω,质量分别为0.1 kg和0.2 kg,两金属棒与金属导轨接触良好且可沿导轨自由滑动。现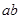 棒在外力作用下,以恒定速度ν=1.5m/s沿着导轨向上滑动,
棒在外力作用下,以恒定速度ν=1.5m/s沿着导轨向上滑动,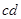 棒则由静止释放。试求:(取g="10" m/s2)
棒则由静止释放。试求:(取g="10" m/s2)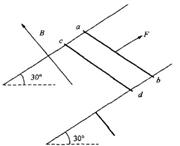
(1)金属棒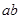 产生的感应电动势;
产生的感应电动势;
(2)闭合回路中的最小电流和最大电流;
(3)金属棒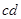 的最终速度。
的最终速度。
参考答案:(1)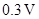 (2)
(2)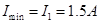 ?
?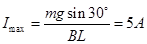 (3)
(3)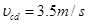
本题解析:(18分)
(1)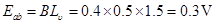 ---------------------------(3分)
---------------------------(3分)
(2)刚释放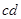 棒时,
棒时,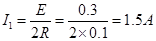 ? ---------------------------(2分)?
? ---------------------------(2分)? 棒受到安培力为:
棒受到安培力为: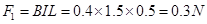 -------------------(1分)
-------------------(1分) 棒受到的重力为:
棒受到的重力为: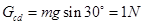 ? ---------------------------(1分)?
? ---------------------------(1分)?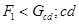 棒沿导轨向下加速运动,即
棒沿导轨向下加速运动,即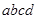 闭合回路的
闭合回路的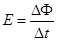 增大;电流也将增大,所以最小电流为:
增大;电流也将增大,所以最小电流为: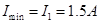 ? ---------------------------(4分)?
? ---------------------------(4分)?
当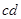 棒的速度达到最大时,同路的电流最大,此时
棒的速度达到最大时,同路的电流最大,此时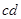 棒的加速度为零。
棒的加速度为零。
由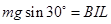 得:
得: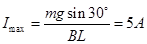 ---------------------------(4分)?
---------------------------(4分)?
(3)由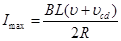 得:
得: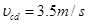 ---------------------------(3分)
---------------------------(3分)
本题考查的是电磁感应定律和力学综合的问题,首先根据电磁感应定律计算出感应电动势;然后根据安培力的计算和力学规律计算出最大最小电流;最后根据欧姆定律计算出电压;
本题难度:一般
4、选择题 如图所示,一个带少量正电的小球沿着水平光滑绝缘的桌面向右运动,其速度方向垂直于一个水平方向的匀强磁场,小球飞离桌面边缘后落到水平地板上,设其在空中飞行时间为t1,水平射程为s1,着地时速率为v1,撤去磁场,其余条件不变,小球飞行时间为t2,水平射程为s2,着地时速率为v2,若不计空气阻力,则
[? ]
A.s1>s2
B.t1>t2
C.v1>v2
D.v1=v2
参考答案:ABD
本题解析:
本题难度:一般
5、选择题 如图一混合正离子束先后通过正交电场磁场区域Ⅰ和匀强磁场区域Ⅱ,如果这束正离子束流在区域Ⅰ中不偏转,进入区域Ⅱ后偏转半径又相同,则说明这些正离子具有相同的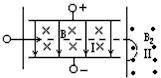
[? ]
A、速度
B、质量
C、电荷
D、荷质比
参考答案:AD
本题解析:
本题难度:一般