时间:2018-10-13 00:21:46
1、计算题 (12分)如图所示,在相距为L,长为3L的平行金属板中间区域存在正交的匀强电场和匀强磁场,磁感应强度为B(方向未画),电场方向竖直向下。有一群均匀分布的同种带电粒子,以相同速度从两板间水平射入,经过时间t,粒子沿直线穿过该区域。若在粒子进入板间时,撤去电场保留磁场,粒子恰好全部打在板上。不计粒子的重力,不考虑粒子之间的相互作用,粒子对原来电场和磁场的影响不计。试求: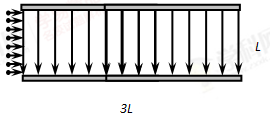
(1)该区域电场强度E大小;
(2)该粒子的比荷q/m ;
(3)若粒子进入时撤去磁场保留电场,则射出该区域的粒子数为总数的多少?
2、计算题 如图Ox、Oy、Oz为相互垂直的坐标轴,Oy轴为竖直方向,整个空间存在竖直向下的匀强磁场,磁感应强度大小为B。现有一质量为、电量为q的小球从坐标原点O以速度v0沿Ox轴正方向抛出(不计空气阻力,重力加速度为g)。求:
(1)若在整个空间加一匀强电场E1,使小球在xOz平面内做匀速圆周运动,求场强E1和小球运动的轨道半径;
(2)若在整个空间加一匀强电场E2,使小球沿Ox轴做匀速直线运动,求E2的大小;
(3)若在整个空间加一沿y轴正方向的匀强电场,求该小球从坐标原点O抛出后,经过y轴时的坐标y和动能Ek; 
3、选择题 如图13-2-2所示为理想变压器,三个灯泡L1、L2、L3都标有“5V,5W”,L4标有“5V,10W”,若它们都能正常发光,则变压器原、副线圈匝数比n1∶n2和ab间电压应为 (?)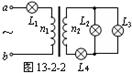
A.2∶1,25V
B.2∶1,20V
C.3∶2,15V
D.1∶2,20V
4、计算题 (19分)如图所示装置中,区域Ⅰ和Ⅲ中分别有竖直向上和水平向右的匀强电场,电场强度分别为E和E/2;Ⅱ区域内有垂直向外的水平匀强磁场,磁感应强度为B。一质量为m、带电量为q的带负电粒子(不计重力)从左边界O点正上方的M点以速度v0水平射入电场,经水平分界线OP上的A点与OP成60°角射入Ⅱ区域的磁场,并垂直竖直边界CD进入Ⅲ区域的匀强电场中。求:
(1)粒子在Ⅱ区域匀强磁场中运动的轨道半径;
(2)O、M间的距离;
(3)粒子从M点出发到第二次通过CD边界所经历的时间。
5、选择题 如图所示,某空间存在正交的匀强磁场和匀强电场,电场方向水平向右,磁场方向垂直纸面向里,一带电微粒由A 点进入电磁场并刚好能沿AB直线向上运动,则该微粒在A、B两点的动能Ek和电势能Ep的关系是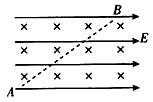
[? ]
A.EkA< EkB
B.EkA>EkB
C.EpA<
D.EpA> EpB