时间:2018-10-11 01:30:14
1、计算题 (18分)如图所示,x轴上方有一匀强磁场,磁感应强度为B,磁场方向垂直于纸面向里。X轴下方有一匀强电场,电场强度为E、方向与y轴的夹角θ=45°且斜向上方。现有一质量为m电量为q的正离子,以速度v0由y轴上的A点沿y轴正方向射入磁场,该离子在磁场中运动一段时间后从x轴上的C点(图中未画出)进入电场区域,离子经C点时的速度方向与电场方向相反。 不计离子的重力,设磁场区域和电场区域足够大, 求:
(1)C点的坐标;
(2)离子从A点出发到第三次穿越x轴时的运动时间;
(3)回答:离子从第三次过x轴到第四次过x轴的过程在做什么运动。并大致画出离子前四次穿越x轴在磁场和电场区域中的运动轨迹。
参考答案:(1)C点坐标为(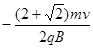 ,0)。(2)
,0)。(2)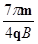 +
+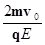 ;(3)类平抛运动,轨迹如下图:
;(3)类平抛运动,轨迹如下图:
本题解析:(1)磁场中带电粒子在洛仑兹力作用下做圆周运动,故有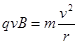 ①
①
由几何知识知,xC= (r+rcos450)=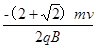 ③
③
故,C点坐标为(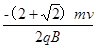 ,0) ③
,0) ③
(2)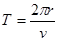 =
=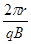 ④
④
设粒子从A到C的时间为t1,设粒子从A到C的时间为t1,由题意知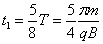 ⑤
⑤
设粒子从进入电场到返回C的时间为t2,其在电场中做匀变速运动,由牛顿第二定律和运动学知识,有 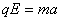 ⑥
⑥
及 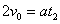 ⑦
⑦
联立⑥⑦解得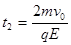 ⑧
⑧
设粒子再次进入磁场后在磁场中运动的时间为t3,由题意知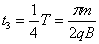 ⑨
⑨
故而,设粒子从A点到第三次穿越x轴的时间为
考点:带电粒子在电场中的运动(类平抛运动)、带电粒子在匀强磁场中的运动
本题难度:困难
2、选择题 如图为云室中某粒子穿过铅板P前后的轨迹,云室中匀强磁场的方向与轨迹所在平面垂直。由此可知此粒子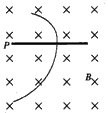
[? ]
A.一定带正电
B.一定带负电
C.不带电
D.可能带正电,也可能带负电
参考答案:A
本题解析:
本题难度:一般
3、选择题 长为L,间距也为L的两平行金属板间有垂直纸面向里的匀强磁场,如图,磁感应强度为B,今有质量为m、带电量为q的正离子从平行板左端中点以平行于金属板的方向射入磁场。欲使离子不打在极板上,入射离子的速度大小应满足的条件是
①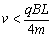 ②
②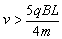 ③
③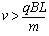 ④
④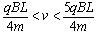
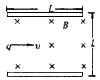
[? ]
A.①②
B.①③
C.②③
D.②④
参考答案:A
本题解析:
本题难度:一般
4、选择题 如图所示,在X>0,Y>0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于XOY平面向里,大小为B.现有一质量为m、电量为q的带正电粒子,从在x轴上的某点P沿着与x轴成300角的方向射入磁场.不计重力的影响,则下列有关说法中正确的是( )
A.只要粒子的速率合适,粒子就可能通过坐标原点
B.粒子一定不可能通过坐标原点
C.粒子在磁场中运动所经历的时间可能为
| πm Bq |
| πm 6Bq |

参考答案:AB、粒子由P点成30°角入射,则圆心在过P点与速度方向垂直的方向上,如图所示,粒子在磁场中要想到达O点,转过的圆心角肯定大于180°,而因磁场为有界,故粒子不可能通过坐标原点,故A错误,B正确;
C、由于P点的位置不定,所以粒子在磁场中的运动圆弧对应的圆心角也不同,最大的圆心角时圆弧与y轴相切时即300°,则运动的时间为56T=5πm3qB;
而最小的圆心角为P点从坐标原点出发,圆心角为120°,所以运动时间为T3=2πm3qB,故粒子在磁场中运动所经历的时间为2πm3qB≤t≤5πm3qB,故C正确,D错误
故选:BC
本题解析:
本题难度:简单
5、简答题 如图,坐标系xOy在竖直平面内,第一象限内分布匀强磁场,磁感应强度大小为B,方向垂直纸面向外;第二象限内分布着沿x轴正方向的水平匀强电场,场强大小E=
| B2qL 6m |
2 |

参考答案:(1)设粒子进入磁场的速度为v,由动能定理得qEL=12mv2
又E=B2qL6m
解得:v=
本题解析:
本题难度:一般