时间:2018-10-11 01:08:41
1、选择题 如图所示,有一个正方形的匀强磁场区域abcd,e是ad的中点,f是cd的中点,如果在a点沿对角线方向以速度v射入一带负电的粒子,恰好从e点射出,粒子的重力不计,则( )
A.如果粒子的速度增大为原来的二倍,磁场的磁感应强度不变,也将从e点射出
B.如果粒子的速度增大为原来的二倍,磁场的磁感应强度也变为原来的二倍,将从d点射出
C.如果粒子的速度不变,磁场的磁感应强度变为原来的
| 1 4 |

参考答案:
A、如果粒子的速度增大为原来的二倍,磁场的磁感应强度不变,由半径公式r=mvqB可知,半径将为原来的2倍,粒子不可能从e点射出.故A错误.
B、如果粒子的速度增大为原来的二倍,磁场的磁感应强度也变为原来的二倍,由半径公式r=mvqB可知,半径不变,仍从e点射出.故B错误.
C、设正方形的边长为2a,则粒子从e点射出时,轨迹半径为
本题解析:
本题难度:一般
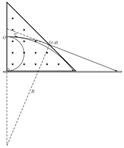
2、选择题 如图所示,边长为L的等边三角形ABC为两有界匀强磁场的理想边界,三角形内的磁场方向垂直纸面向外,磁感应强度大小为B,三角形外的磁场(足够大)方向垂直纸面向里,磁感应强度大小也为B.把粒子源放在顶点A处,它将沿∠A的角平分线发射质量为m、电荷量为q、初速度为v0的带电粒子(粒子重力不计).若从A射出的粒子
①带负电,v0=
| qBL m |
| qBL 2m |
| qBL m |
| qBL 2m |

参考答案:粒子在磁场中做匀速圆周运动,洛伦兹力提供圆周运动的向心力,如图所示,
当v0=qBLm
所以有:qvB=mv2r
?r=mvqB=L
根据几何关系可知作出运动轨迹,
根据轨迹可知,当电荷带正电,粒子经过一个周期到达C点,即为t3;
当粒子带负电,粒子经过16T第一次到达C点,即为t1.
当v0=qBL2m
所以有:qvB=mv2r
?r=mvqB=L2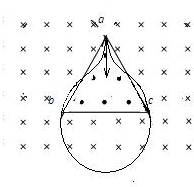
根据轨迹可知,当电荷带正电,粒子经过56T到达C点,即为t4;
当粒子带负电,粒子经过13T第一次到达C点,即为t2.
所以B正确,ACD错误.
故选:B.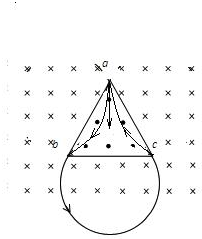
本题解析:
本题难度:简单
3、选择题 如图所示,质量为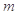 、带电量为
、带电量为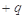 的三个相同的带电小球A、B、C,从同一高度以初速度
的三个相同的带电小球A、B、C,从同一高度以初速度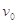 水平抛出,B球处于竖直向下的匀强磁场中,C球处于垂直纸面向里的匀强电场中,它们落地的时间分别为
水平抛出,B球处于竖直向下的匀强磁场中,C球处于垂直纸面向里的匀强电场中,它们落地的时间分别为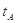 、
、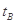 、
、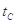 ,落地时的速度大小分别为
,落地时的速度大小分别为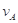 、
、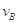 、
、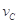 ,则以下判断正确的是:( )
,则以下判断正确的是:( ) 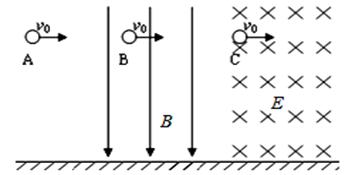
A.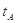 =
=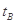 =
=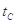 B.
B.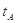 =
=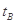 >
>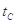 C.
C.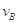 >
>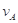 =
=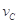 D.
D.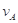 =
=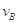 <
<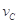
参考答案:AD
本题解析:根据题意可知:A球只有重力做功,竖直方向上做自由落体运动;B球除重力之外还受到洛伦兹力作用,因为B得水平速度不变,故B的洛伦兹力总是水平方向的且垂直纸面向里的,不影响重力方向,所以竖直方向也做自由落体运动.但洛伦兹力不做功,也只有重力做功;C球除重力做功外,还受到垂直纸面向里的电场力作用,竖直方向做自由落体运动,而且电场力对其做正功.
所以三个球竖直方向都做自由落体运动,下落的高度又相同,故下落时间相同,则有tA=tB=tC.故A正确,B错误.根据动能定理可知:A、B两球合力做的功相等,初速度又相同,所以末速度大小相等,而C球合外力做的功比A、B两球合外力做的功大,而初速度与A、B球的初速度相等,故C球的末速度比A、B两球的末速度大,即vA=vB<vC.故C错误,D正确;故选AD.
考点:带电粒子在匀强磁场及在匀强电场中的运动,动能定理的应用.
本题难度:一般
4、简答题 一足够长的矩形区域abcd内有磁感应强度为B,方向垂直纸面向里的匀强磁场,矩形区域的左边界ad宽为L,现从ad中点O垂直于磁场射入一带电粒子,速度大小为v0,方向与ad边夹角为θ=30°,如图所示.已知粒子的电荷量为q,质量为m(重力忽略不计).
(1)若粒子带负电,且恰好能从d点射出磁场,求v0的大小;
(2)若粒子带正电,使粒子能从ab边射出磁场,求v0的取值范围,以及此范围内粒子在磁场中运动时间t的范围.
参考答案:(1)若粒子带负电,且恰好能从d点射出磁场,它运动的轨迹如图1,
则运动的半径:R=L2,
运动的过程洛伦兹力提供向心力,得:qv0B=mv20R
整理得:ν0=BqL2m
(2)若粒子带正电,粒子运动的轨迹如右图所示,当粒子的速度大于与R1相对应的速度v1时,粒子将从dc边射出.
由几何关系可得:R1=L①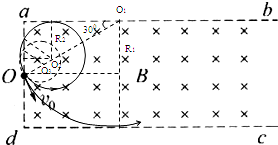
由洛仑兹力和向心力公式可得:qv1B=mv21R1 ②
当粒子的速度小于与R2相对应的速度v2时,粒子将从ad边射出.
由几何关系可得:12L-R2=12R2 ③
由③式解得:R2=13L ④
由洛仑兹力和向心力公式可得:qv2B=mv22R2 ⑤
将①④式分别代入②⑤式可解得:v1=qBLm;v2=qBL3m ⑥
所以v0的取值范围是qBL3m≤v0≤qBLm ⑦
从图中可以看出,当轨迹的半径对应R1时从ab边上射出使用的时间最短,此时对应的圆心角为:
θ=180°-30°=150°
由公式可得:T=2πRv=2πmqB⑧
根据周期与运动时间的关系得:θ360°=t1T
整理得:t1=5πm6qB ⑨
粒子在磁场中运动的时间最长,其做圆周运动的圆心角必然最大,在答图中,当粒子的速度小于v2时,粒子从ad边的不同位置射出时,其半径虽不同,但圆心角的夹角都是300°=56×2π,所以粒子在磁场中的运动时间也是5T6,此即粒子在磁场中运动的最长时间.
所以粒子运动的最长时间为:t2=5T6=5πm3qB⑩
与粒子在磁场中运行时间相对应的t的大小范围是5πm6Bq<t≤5πm3Bq:
答:(1)ν0=BqL2m(2)v0的取值范围BqL3m≤ν0≤BqLm,粒子在磁场中运动时间t的范围5πm6Bq<t≤5πm3Bq.
本题解析:
本题难度:简单
5、计算题 有一等腰直角ABC三角形区域,直角边长为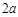 。在该区域,有一垂直纸面向内磁感应强度为
。在该区域,有一垂直纸面向内磁感应强度为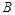 的匀强磁场。一束质量为
的匀强磁场。一束质量为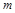 、电荷量为
、电荷量为 ,带负电粒子以不同速度从中点
,带负电粒子以不同速度从中点 垂直直角边射入该磁场区域,在另一直角边放置一块荧光屏,如图所示。重力不计,求
垂直直角边射入该磁场区域,在另一直角边放置一块荧光屏,如图所示。重力不计,求
(1)当粒子以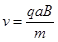 入射时,求粒子在荧光屏上光斑的位置及在磁场中运动的时间。
入射时,求粒子在荧光屏上光斑的位置及在磁场中运动的时间。
(2)荧光屏AB区域上光斑的分布区域。
(3)若把磁场更换成沿AC方向的场强为E的匀强电场,当粒子以 入射时,求粒子在荧光屏上光斑的位置
入射时,求粒子在荧光屏上光斑的位置
(4)把磁场更换成沿AC方向的场强为E的匀强电场,荧光屏AB区域上光斑的分布区域。
参考答案:(1) (2)
(2)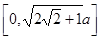 (3)AB边的中点位置(4)
(3)AB边的中点位置(4)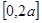
本题解析:(1)根据带电粒子在磁场中运动规律,可得 
所以粒子打在荧光屏的位置位于AB边的中点位置,所用的时间为
(2)在磁场区域内,为了求出荧光屏最远处亮点坐标。如图可得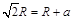
求出相切位置对应的半径
对应的最远坐标为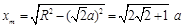
所以荧光屏AB区域上光斑分布区域为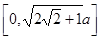
(3)根据带电粒子在电场中运动规律,可得 

可以求得:
粒子打在荧光屏的位置位于AB边的中点位置
(4)带点粒子在电场中荧光屏最远处亮点位置时,平抛的抛物线应该和BC边相切即BC应该是最远粒子速度的方向,根据平抛物体的运动规律,速度的反向延长线交于水平位移的重点,所以粒子最远达到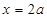 处。
处。
所以荧光屏AB区域上光斑分布区域为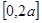
考点:此题考查了带电粒子在磁场中的运动。
本题难度:一般