时间:2018-10-11 01:06:47
1、计算题 一束光波以45°的入射角，从AB面射入如图所示的透明三棱镜中，棱镜折射率n=
，试求光进入AB面的折射角，并在图中画出该光束在棱镜中的光路。
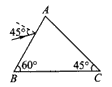
参考答案：解：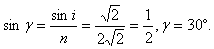
图“略”（其中由几何关系，画出光线在AC面上的入射角i=45°，由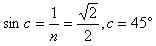
，光在AC面发生全反射，并垂直于BC面射出）
本题解析：
本题难度：一般
2、选择题 如图所示，截面为等腰三角形的棱镜顶角α=41.30°，一束白光以较大的入射角θ从棱镜的一侧射入，通过棱镜后从另一个侧面射出，在光屏上形成由红到紫的彩色光带．当入射角θ逐渐减小到零的过程中，请根据下表中该棱镜材料对各种色光的折射率和发生全反射的临界角，判断光屏上彩色光带的变化情况（ ）
| 色光 | 红 | 橙 | 黄 | 绿 | 蓝 | 紫 折射率 1.513 1.514 1.517 1.519 1.528 1.532 临界角 41.37° 41.34° 41.23° 41.17° 40.88° 40.75° |
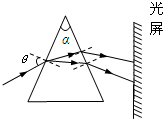
参考答案：由表格数据看出，紫光的折射率最大，临界角最小，当入射角θ逐渐减小到零的过程中，光线射到棱镜右侧面的入射角减小，紫光的入射角最先达到临界角，发生全反射，最先消失．
当入射角θ减小到零时，光线射到棱镜右侧面的入射角等于α=41.30°，小于红光与橙光的临界角，所以这两种光不发生全反射，仍能射到光屏上．故最后光屏上只剩下红、橙两种色光．故B正确，ACD错误．
故选B
本题解析：
本题难度：一般
3、填空题 激光在真空中传播速度为c，进入某种均匀介质时，传播速度变为真空中的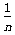
，则激光在此均匀介质中的波长变为在真空中波长的______倍；某激光光源的发光功率为P，发射激光的波长为λ，该激光进入上述介质时由于反射，入射能量减少了10% ，该激光在这种介质中形成的光束横截面积为S，则在垂直于光束传播方向的截面内，单位时间内通过单位面积的光子个数为______。（已知普朗克常量为h）
参考答案：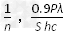
本题解析：
本题难度：一般
4、计算题 如图所示，为一玻璃圆柱体的截面图，其半径为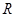
，
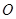为圆柱截面的圆心，AB为截面圆的直径。在B点放一个能发某种单色光的点光源，照射到直径AB上方，只有圆弧AMN段有光线折射出来，其中从M点折射出的光线恰好平行AB，已知∠ABM=
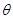。求：直线BN的长度。（用R、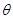表示）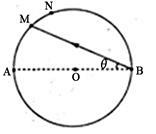
参考答案：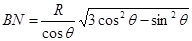
本题解析：设光线BM在M点发生折射对应的入射角为i，折射角为r，
由几何知识可知，i＝θ，r＝2θ， (1分)
根据折射定律得：
? (1分)
代入数据得：n=2cosθ? (1分)
光线BN恰好在N点发生全反射，则∠BNO为临界角C，有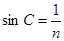
?(1分)
由几何知识可知，等腰三角形NOB中，BN的距离：
BN="2RcosC" ?(1分)
联立求得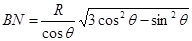：? (1分)
本题难度：一般
5、简答题 有一个很大的湖，岸边（可视湖岸为直线）停放着一艘小船，缆绳突然断开，小船被风刮跑，其方向与湖岸成15°角，速度为2.5km/h。同时岸上一人从停放点起追赶小船，已知他在岸上跑的速度为4.0km/h，在水中游的速度为2.0km/h，问此人能否追及小船？
参考答案：人能追上小船
本题解析：费马原理指出：光总是沿着光程为极小值的路径传播。据此就将一个运动问题通过类比法可转化为光的折射问题。
如图3所示，船沿OP方向被刮跑，设人从O点出发先沿湖岸跑，在A点入水游到OP方向的B点，如果符合光的折射定律，则所用时间最短。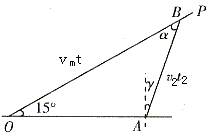
图3
根据折射定律：
解得
在这最短时间内，若船还未到达B点，则人能追上小船，若船已经通过了B点，则人不能追上小船，所以船刚好能到达B点所对应的船速就是小船能被追及的最大船速
。
根据正弦定理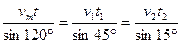
又
由以上两式可解得：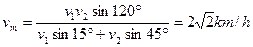
此即小船能被人追上的最大速度，而小船实际速度只有2.5km/h，小于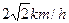
，所以人能追上小船。
本题难度：简单