时间:2018-10-11 00:08:02
1、简答题 在纳米技术中需要移动或修补原子,必须使在不停地做热运动(速率约几百米每秒)的原子几乎静止下来且能在一个小的空间区域内停留一段时间,为此已发明了“激光致冷”技术.若把原子和入射光子分别类比为一辆小车和一个小球,则“激光致冷”与下述的模型很类似.
一辆质量为m的小车(一侧固定一轻弹簧),如图所示,以速度v0水平向右运动,一动量大小为p,质量可以忽略的小球水平向左射入小车并压缩弹簧至最短,接着被锁定一定时间ΔT,再解除锁定使小球以大小相同的动量p水平向右弹出,紧接着不断重复上述过程,最终小车将停下来.设地面和车厢均为光滑,除锁定时间ΔT外.不计小球在小车上运动和弹簧压缩、伸长的时间,求:
(1)小球第一次入射后再弹出时,小车的速度的大小和这一过程中小车动能的减少量;
(2)从小球第一次入射开始到小车停止运动所经历的时间.
参考答案:
(1)2Pv0- ?(2)
?(2) ΔT
ΔT
本题解析:
(1)设发生第一次作用后小车的速度为v1,由动量守恒有
mv0-P=P+mv1,v1=v0- ,
,
动能的减小量
ΔEk= m(
m( )=2Pv0-
)=2Pv0- .
.
(2)设发生第二次作用后,小车的速度为v2,由动量守恒有
mv1-P=P+mv2,v2=v1- =v0-2×
=v0-2× ,
,
所以发生第n次作用后,小车的速度
vn=v0-n· ,
,
当vn=0时,n= ,
,
故小车共运动的时间T=nΔT= ΔT.
ΔT.
本题难度:一般
2、填空题 如图所示,一个运动的中子与一个静止的中子发生弹性碰撞,碰撞过程中动量______(“一定”、“可能”或“一定不”)守恒,碰撞后A中子______(“静止”“向右运动”或“向左运动”).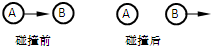
参考答案:一个运动的中子与一个静止的中子发生弹性碰撞,由动量守恒定理可得:碰撞过程中动量是守恒的.
因为发生的是弹性碰撞,且两个中子质量是一样的,所以运动的A中子的能量无损失的传递给B中子,故碰撞后:A静止,B速度与A原来的速度相等.
故答案为:一定,静止.
本题解析:
本题难度:一般
3、计算题 【选修3-5选做题】
如图所示,平放在水平面上的轻质弹簧的一端固定在竖直墙上,质量为m1的光滑弧形槽静止在光滑水平面上,底部与水平面平滑连接。一个质量为m2的小球从槽h高处由静止开始下滑,要使小球能与弧形槽发生第二次作用,m1、m2应满足怎样的条件?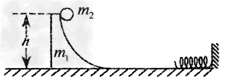
参考答案:解:设弧形槽与小球第一次分离后的速度大小分别为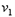 和
和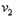
弧形槽和小球在水平方向满足动量守恒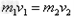
小球与弹簧发生作用后以原速率返回,要使小球和弧形槽发生第二次作用则满足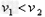
所以弧形槽和小球的质量应满足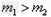
本题解析:
本题难度:一般
4、计算题 甲、乙两辆小车质量分别为m1=50kg和m2=30kg,质量m=30kg的小孩站在甲车上。两车在光滑轨道上相向运动,车速V1=3m/s,V2=4m/s,为避免两车相撞,小孩至少以多大的水平速度(相对地面)跳到乙车上?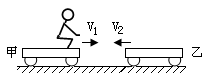
参考答案:“跳、落”是常见的内力作用方式,动量是状态量,抓住跳之前和跳之后、落之前和落之后的状态。规定向右为正方向,小孩的速度用u表示。
以甲车、小孩为系统:(m1+m)V1=m1V1/+mu?(1) (3分)
以小孩、乙车为系统:mu+m2(-V2)=(m+m2)V2/?(2) (3分)
两车不撞:V1/≤V2/?(2分)
得u≥6.2m/s,即小孩至少以6.2m/s的水平速度跳到乙车上才能避免两车相撞。(2分)
本题解析:略
本题难度:简单
5、选择题 两球A、B在光滑水平面上沿同一直线,同一方向运动,mA="1" kg,mB="2" kg,VA="6" m/s,VB="2" m/s。当A追上B并发生碰撞后,两球A、B速度的可能值是(?)
A. VA′="5" m/s, ?VB′="2.5" m/s? B. VA′="2" m/s, VB′="4" m/s
C. VA′=-4 m/s, VB′="7" m/s? D. VA′="7" m/s, VB′="1.5" m/s
参考答案:B
本题解析:考虑实际情况,碰撞后A球速度不大于B球的速度,因而AD错误,BC满足;两球碰撞过程,系统不受外力,故碰撞过程系统总动量守恒,ABCD均满足;根据能量守恒定律,碰撞后的系统总动能应该小于或等于碰撞前的系统总动能,碰撞前总动能为22J,B选项碰撞后总动能为18J,C选项碰撞后总动能为57J,故ACD错误,B满足;
故选B.
点评:本题碰撞过程中动量守恒,同时要遵循能量守恒定律,不忘联系实际情况,即后面的球不会比前面的球运动的快!
本题难度:一般