时间:2018-10-02 04:09:09
1、计算题 如下图所示，竖直平面（纸面）内有直角坐标系xOy，x轴沿水平方向。在x≤O的区域内存在方向垂直于纸面向里，磁感应强度大小为B1的匀强磁场。在第二象限紧贴y轴固定放置长为l、表面粗糙的不带电绝缘平板，平板平行于x轴且与x轴相距h。在第一象限内的某区域存在方向相互垂直的匀强磁场（磁感应强度大小为B2、方向垂直于纸面向外）和匀强电场（图中未画出）。一质量为m、不带电的小球Q从平板下侧A点沿x轴正向抛出；另一质量也为m、带电量为q的小球P从A点紧贴平板沿x轴正向运动，变为匀速运动后从y轴上的D点进入电磁场区域做匀速圆周运动，经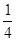
圆周离开电磁场区域，沿y轴负方向运动，然后从x轴上的K点进入第四象限。小球P、Q相遇在第四象限的某一点，且竖直方向速度相同。设运动过程中小球P电量不变，小球P和Q始终在纸面内运动且均看作质点，重力加速度为g。求：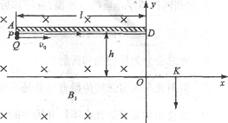
（1）匀强电场的场强大小，并判断P球所带电荷的正负；
（2）小球Q的抛出速度v0的取值范围；
（3）B1是B2的多少倍？
参考答案：（1）E=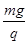
??P球带正电 （2）0＜v0＜
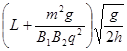?（3）
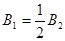
本题解析：根据题意，受力分析如图所示。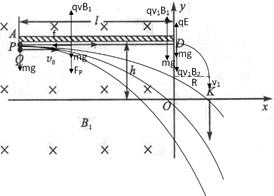
（1）根据题述条件，带电小球P在电磁复合场中做匀速圆周运动，必有重力与电场力平衡，设所求匀强电场的场强大小为E，有mg=qE?①
即E=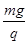?②
小球P紧贴平板运动，其所受洛伦兹力必竖直向上，根据左手定则可知，小球P带正电。
（2）设小球P紧贴平板匀速运动的速度为v，此时洛伦兹力与重力平衡，有B1qv=mg?③
设小球P以速度v在电磁场区域内做圆周运动的半径为R，有B2qv=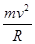
?④
设小球Q和小球P在第四象限相遇点的坐标为（x，y），有x=R，y＜0?⑤
设小球Q运动到相遇点的时间为t0，水平方向的位移为s，竖直方向的位移为d，有
s=v0t0?⑥
d=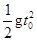
?⑦
由题意得，x=s-l，y=h-d?⑧
联立各方程，由题意可知，v0大于0，得0＜v0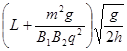＜?⑨
（3）小球Q做平抛运动，要满足题设要求，则运动到小球P穿出磁场区域时的同一水平高度时的W点时，其竖直方向的速度vy和竖直位移yQ必修满足
vy=v??⑩
yQ=R ?（11）
设小球Q运动到W点的时间为t，由平抛运动，有
vy=gt??⑩
yQ=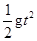
??（11）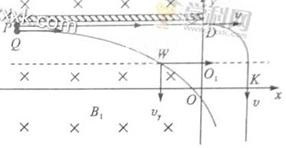
联立相关方程，解得。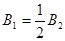
【考点定位】带电小球在混合场中的运动、平抛运动、匀速圆周运动。
本题难度：一般
2、选择题 如图所示，匀强电场E方向竖直向下，水平匀强磁场B垂直纸面向里，三个油滴a、b、c带有等量同种电荷．已知a静止，b、c在纸面内按图示方向做匀速圆周运动（轨迹未画出）．忽略三个油滴间的静电力作用，比较三个油滴的质量及b、c的运动情况，以下说法中正确的是（ ）
A．三个油滴质量相等，b、c都沿顺时针方向运动
B．a的质量最大，c的质量最小，b、c都沿逆时针方向运动
C．b的质量最大，a的质量最小，b、c都沿顺时针方向运动
D．三个油滴质量相等，b沿顺时针方向运动，c沿逆时针方向运动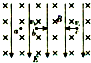
参考答案：三个油滴带等量同种电荷，由a静止可知带负电，电场力等于重力，b、c做圆周运动，电场力也等于重力．所以三者质量相等，由左手定则可知b、c都沿顺时针方向运动．故A正确，B、C、D错误．
故选A．
本题解析：
本题难度：简单
3、选择题 在空间某一区域中既存在匀强电场，又存在匀强磁场.有一带电粒子，以某一速度射入到该区域中(不计带电粒子受到的重力)，则该带电粒子在区域中的运动情况可能是（?）
A．做匀速直线运动
B．做匀速圆周运动
C．做匀变速直线运动
D．做匀变速曲线运动
参考答案：AC
本题解析：当粒子所受电场力与洛仑兹力平衡时，粒子做匀速直线运动，选项A正确；由于电场力与洛仑兹力的区别可知，粒子不可能做匀速圆周运动，选项B错误；当粒子速度与磁场方向共线时，粒子不受洛仑兹力，粒子将做匀变速直线运动，选项C正确；同理选项D错误；故选AC
点评：本题难度较小，由于洛仑兹力方向时刻与速度垂直，因此粒子不可能做匀变速曲线运动，抓住洛仑兹力作用特点是关键
本题难度：简单
4、计算题 如图甲所示，两平行金属板A、B的板长l＝0.20 m，板间距d＝0.20 m，两金属板间加如图乙所示的交变电压，并在两板间形成交变的匀强电场，忽略其边缘效应。在金属板右侧有一方向垂直于纸面向里的匀强磁场，其左右宽度D＝0.40 m，上下范围足够大，边界MN和PQ均与金属板垂直，匀强磁场的磁感应强度B＝1.0×10－2 T。现从t＝0开始，从两极板左端的中点O处以每秒钟1 000个的速率不停地释放出某种带正电的粒子，这些粒子均以v0＝2.0×105 m/s的速度沿两板间的中线OO′射入电场，已知带电粒子的比荷＝1.0×108 C/kg，粒子的重力和粒子间的相互作用都忽略不计，在粒子通过电场区域的极短时间内极板间的电压可以看作不变。求：
（1）t＝0时刻进入的粒子，经边界MN射入磁场和射出磁场时两点间的距离；
（2）在电压变化的第一个周期内有多少个带电的粒子能进入磁场；
（3）何时由O点进入的带电粒子在磁场中运动的时间最长？最长时间为多少？（π≈3） 
参考答案：解：（1）t＝0时刻电压为零，粒子匀速通过极板
由牛顿第二定律Bqv0＝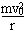
得：r＝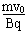
＝0.2m＜D
所以出射点到入射点的距离为s＝2r＝0.4m
（2）考虑临界情况：粒子刚好不能射出电场
对类平抛过程：y＝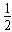
at2＝
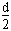，a＝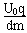
，l＝v0t
联立解得U0＝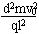
＝400 V
当|uAB|＜U0时，粒子可以射出电场，根据比例关系得
第一个周期内能够出射的粒子数为n＝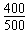
×1 000×T＝3 200个
（3）当粒子向下偏转，出射后恰好与磁场右边界相切时，粒子在磁场中的圆心角最大，时间最长。设粒子在电场中的偏转角为θ：则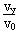
＝tanθ，v＝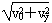
磁场中圆周运动：Bqv＝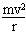
几何关系r＋rsinθ＝D
联立得：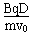
＝1＋sinθ
＝
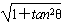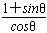
代入数据解得：sinθ＝0.6，即θ＝37°
又因为vy＝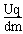
·t＝v0tan37°，l＝v0t
解得：U＝300 V
所以对应的入射时刻为t＝4n＋0.6（s）或t＝4n＋1.4（s）（n＝0、1、2…）
在磁场中运动的最长时间为Δ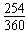t＝
T＝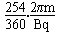
≈4.2×10－6 s
本题解析：
本题难度：困难
5、计算题 （12分）如图所示，质量
kg的小球，带有
C的正电荷，套在一根与水平方向成
角的足够长绝缘杆上。小球可以沿杆滑动，与杆间的动摩擦因数
，这个装置放在磁感应强度
T的匀强磁场中，求小球无初速释放后沿杆下滑的最大加速度和最大速度。（g=10m/s2）
参考答案：
解：开始阶段小球速度小，洛伦兹力较小，杆对球支持力垂直杆斜向上，且逐渐减小，当速度达到某值后，支持力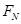
为零，杆对球的摩擦力也减为零，此时球的加速度最大.
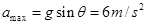…………………………①
此后杆对球的支持力垂直于杆向下且随速度增大而增大，当摩托力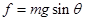
时达到最大速度，根据牛顿第二定律得：
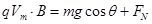…………………………②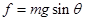…………………………③
且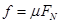
……………………④
由②③④解出：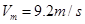
本题解析：略
本题难度：一般