时间:2018-10-02 04:07:16
1、选择题 下列说法中正确的是
[? ]
A.带电粒子在磁场中一定受到磁场力
B.通电导线在磁场中一定受到磁场力
C.运动的带电粒子在匀强磁场中一定做匀速圆周运动
D.运动的带电粒子在磁场中可能不受磁场力
参考答案:D
本题解析:
本题难度:简单
2、选择题 .两条通电的直导线互相垂直,如图15-2-13所示,但两导线相隔一小段距离,其中导线AB是固定的,另一条导线CD能自由转动.它们通以图示方向的直流电时,CD导线将( )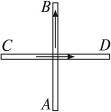
?图15-2-13
A.逆时针方向转动,同时靠近导线AB
B.顺时针方向转动,同时靠近导线AB
C.逆时针方向转动,同时离开导线AB
D.顺时针方向转动,同时离开导线AB
参考答案:A
本题解析:由安培定则可知直线电流产生的磁场是以直线电流为圆心的同心圆,AB中电流所产生的磁场在CD导线所在平面内的磁感线如图甲所示(俯视图).在图示的M、N两点的磁感应强度对导线CD中的电流的力的作用如图乙所示,由左手定则可知,CD通电导线在M点受到的磁场力垂直于纸面向里,在N点受到磁场力垂直于纸面向外.由于磁场的对称性,M、N两点的磁场力大小相等、方向相反,使得CD通电导线在图甲上做逆时针旋转,即CD电流将会转到与AB同向的位置.在图乙中,CD中的电流所受到磁场力由左手定则可知,CD将向AB靠近. ?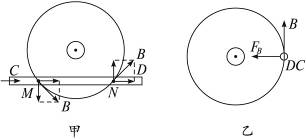
本题难度:简单
3、选择题 带电粒子进入云室会使云室中的气体电离,从而显示其运动轨迹,图是在有匀强磁场的云室中观察到的粒子的轨迹,a和b是轨迹上的两点,匀强磁场B垂直纸面向里.该粒子在运动时,其质量和电荷量不变,而动能逐渐减少.下列说法正确的是( )
A.粒子先经过a点,再经过b点
B.粒子先经过b点,再经过a点
C.粒子带负电
D.粒子带正电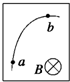
参考答案:粒子在云室中运动时,速度逐渐减小,根据r=mvqB可知其运动轨迹的半径逐渐减小,故粒子运动方向为由a到b,故A正确,B错误;
运动方向由a到b,磁场垂直纸面向里,所受洛伦兹力方向指向运动轨迹内侧,故由左手定则可知该电荷带负电,故C正确,D错误.
故选AC.
本题解析:
本题难度:简单
4、计算题 一质量为m、带电量为q的带电粒子以某一初速射入如图11-2-6所示的匀强磁场中(磁感应强度为B,磁场宽度为L),要使此带电粒子穿过这个磁场,则带电粒子的初速度应为多大?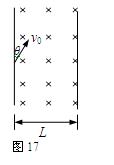
参考答案:a.如果带电粒子带正电,带电粒子在磁场中沿逆时针方向运动,当运动轨迹刚好与磁场右边界相切时,轨道半径R-Rcosθ=L,R=L/(1-cosθ),又R=mv/qB,则速度v=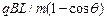 ,即带电粒子要穿过磁场,速度要大于
,即带电粒子要穿过磁场,速度要大于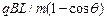 ;
;
b.如果带电粒子带负电,带电粒子在磁场中沿顺时针方向运动,当运动轨迹刚好与磁场右边界相切时,轨道半径R+Rcosθ=L,R=L/(1+cosθ),则速度v=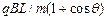 ,带电粒子要穿过磁场,速度要大于
,带电粒子要穿过磁场,速度要大于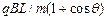 。
。
本题解析:略
本题难度:简单
5、选择题 一同学家中电视机画面的幅度偏小,维修店的技术人员检查后认为是显像管或偏转线圈出了故障(显像管及偏转线圈L如下图所示).那么引起故障的原因可能是
A.电子枪发射能力减弱,电子数减小
B.加速电场的电压过高,电子速率偏大
C.偏转线圈匝间短路,线圈匝数减少
D.偏转线圈的电流过小,偏转磁场减弱
参考答案:CBD
本题解析:电子数目减小,仅能改变画面的清晰度,不会引起画面幅度的偏小,A错误,电视机画面的幅度偏小,则表示电子的偏转减小,所以根据公式 ,
, ,
, 可得,当加速电场的电压过高,电子速率偏大,电子偏转幅度减小,当偏转线圈匝间短路,线圈匝数减少,导致偏转磁场减弱,电子偏转幅度减小,当偏转线圈的电流过小,偏转磁场减弱,电子偏转幅度减小,所以BCD正确,思路分析:电视机画面的幅度偏小,则表示电子的偏转减小,根据公式
可得,当加速电场的电压过高,电子速率偏大,电子偏转幅度减小,当偏转线圈匝间短路,线圈匝数减少,导致偏转磁场减弱,电子偏转幅度减小,当偏转线圈的电流过小,偏转磁场减弱,电子偏转幅度减小,所以BCD正确,思路分析:电视机画面的幅度偏小,则表示电子的偏转减小,根据公式 ,
, ,
, 三式联立分析
三式联立分析
试题点评:本题考查了带电粒子在磁场中的偏转,注意区分电偏转和磁偏转的区别,磁偏转公式
本题难度:困难