时间:2018-10-02 04:03:29
1、计算题 (12分)如图所示,光滑的1/4圆弧轨道AB、EF,半径AO、0′F均为R且水平.质量为m、长度也为R的小车静止在光滑水平面CD上,小车上表面与轨道AB、EF的末端B、E相切.一质量为m的物体(可视为质点)从轨道AB的A点由静止开始下滑,由末端B滑上小车,小车立即向右运动.当小车右端与壁DE刚接触时,物体m恰好滑动到小车右端且相对于小车静止,同时小车与壁DE相碰后立即停止运动但不粘连,物体继续运动滑上圆弧轨道EF,以后又滑下来冲上小车.求:
(1)物体m滑上轨道EF的最高点相对于E点的高度h
(2)水平面CD的长度;
(3)当物体再从轨道EF滑下并滑上小车后,小车立即向左运动.如果小车与壁BC相碰后速度也立即变为零,最后物体m停在小车上的Q点,则Q点距小车右端多远?
参考答案:(1)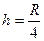 ? (4分)?
? (4分)?
(2) 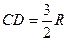 ?(4分)
?(4分)
(3) (4分)
(4分)
本题解析:略
本题难度:简单
2、其他 如图所示,劲度系数为k的轻弹簧,左端连着绝缘介质小球B,右端连在固定板上,放在光滑绝缘的水平面上。整个装置处在场强大小为E、方向水平向右的匀强电场中。现有一质量为m、带电荷量为+q的小球A,从距B球为S处自由释放,并与B球发生碰撞。碰撞中无机械能损失,且A球的电荷量始终不变。已知B球的质量M=3m,B球被碰后作周期性运动,其运动周期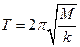 (A、B小球均可视为质点)。
(A、B小球均可视为质点)。
(1)求A球与B球第一次碰撞后瞬间,A球的速度V1和B球的速度V2;
(2)要使A球与B球第二次仍在B球的初始位置迎面相碰,求劲度系数k的可能取值。
参考答案:
(1)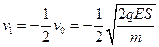 负号表示方向向左
负号表示方向向左  方向向右
方向向右
(2)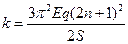 (n="0" 、1 、2 、3 ……)
(n="0" 、1 、2 、3 ……)
本题解析:(1)设A球与B球碰撞前瞬间的速度为v0,
由动能定理得,  ①
①
解得:  ②
②
碰撞过程中动量守恒 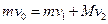 ③
③
机械能无损失,有  ④
④
解得 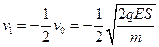 负号表示方向向左
负号表示方向向左  方向向右
方向向右
(2)要使m与M第二次迎面碰撞仍发生在原位置,则必有A球重新回到O处所用的时间t恰好等于B球的
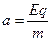 ⑥
⑥ (n="0" 、1 、2 、3 ……) ⑦
(n="0" 、1 、2 、3 ……) ⑦
由题意得: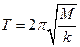 ⑧
⑧
解得: 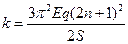 (n="0" 、1 、2 、3 ……)⑨
(n="0" 、1 、2 、3 ……)⑨
本题难度:一般
3、选择题 在光滑的水平面上有质量相等的A、B两球,其动量分别为10kg·m/s与2kg·m/s,方向均向东,且定为正方向,A球在B球后,当A球追上B球发生正碰,则相碰以后,A、B两球的动量可能分别为
A.6kg·m/s,6kg·m/s B.-4kg·m/s,16kg·m/s
C.6kg·m/s,12kg·m/s D.3 kg·m/s,9kg·m/s
参考答案:AD
本题解析:碰撞前后应满足动量守恒,C错。碰前两球动能,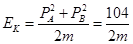 ,碰撞前后能量不增加,只有D选项符合题意。
,碰撞前后能量不增加,只有D选项符合题意。
考点:本题考查了动量守恒定律。
本题难度:一般
4、计算题 如图所示,质量为m=1kg的滑块,以v0=5m/s的水平初速度滑上静止在光滑水平面上的平板车,车的质量M=4kg,车长L=3.6m,滑块在平板车上滑动一段时间后相对小车静止。求滑块与小车的共同速度v。 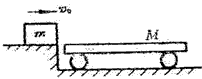
参考答案:解:根据动量守恒定律: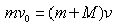
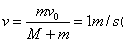
本题解析:
本题难度:一般
5、计算题 如图所示,质量均为m的小滑块P和Q都视作质点,与轻质弹簧相连的Q静止在光滑水平面上。P以某一初速度v0向Q运动并与弹簧发生碰撞,在整个过程中,弹簧具有的最大弹性势能等于多少?P最终的运动速度为多少?
参考答案:速度为0
本题解析:P和Q两者碰撞过程中动量守恒,当两者具有相同速度时,弹簧压缩最多时,弹簧具有最大的弹性势能
m v0=2 m v?①?(2分)
Epm=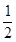 m v02-
m v02-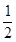 ×2m v2 =
×2m v2 =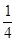 m v02?②?(2分)
m v02?②?(2分)
P和Q两者弹簧压缩后,当弹簧恢复原长,两者分离时,P 的速度最小,
m v0=m v1 +m v2?(2分)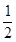 m v02=
m v02=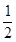 m v12 +
m v12 +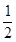 m v22?(2分)
m v22?(2分)
解得v1=0,v2=v0?(1分)
P最终的运动速度为0 .
本题考查动量守恒定律和能量关系,当两物体速度相等时弹性势能最大,弹性势能等于系统动能的减小量
本题难度:一般