时间:2018-10-02 04:03:29
1、计算题 如图所示,在光滑水平桌面上放有长木板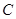 ,
,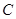 的右端有固定挡板
的右端有固定挡板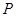 ,木板
,木板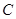 的长度为
的长度为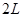 。另有小物块
。另有小物块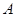 和
和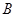 可以在长木板上滑动,
可以在长木板上滑动,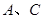 之间和
之间和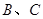 之间的动摩擦因数相同,
之间的动摩擦因数相同,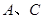 之间和
之间和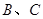 之间的最大静摩擦力等于滑动摩擦力。
之间的最大静摩擦力等于滑动摩擦力。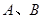 的尺寸以及
的尺寸以及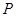 的厚度皆可忽略不计,
的厚度皆可忽略不计,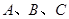 (连同挡板
(连同挡板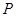 )的质量皆为
)的质量皆为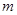 。(1)若
。(1)若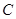 被固定在桌面上,
被固定在桌面上,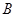 静止放在木板
静止放在木板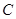 的中央,
的中央,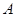 以初速度
以初速度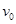 从左端冲上木板
从左端冲上木板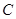 ,物块
,物块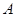 刚好能碰到
刚好能碰到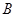 ,求
,求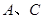 之间的动摩擦因数;(2)若
之间的动摩擦因数;(2)若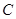 未被固定在桌面上,开始时
未被固定在桌面上,开始时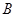 静止放在木板
静止放在木板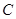 的中央,
的中央,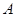 以初速度
以初速度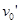 从左端冲上木板
从左端冲上木板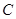 。a.要使物块
。a.要使物块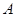 与
与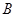 能相碰,初速度
能相碰,初速度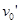 应满足的条件是什么?b.若物块
应满足的条件是什么?b.若物块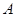 与
与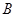 发生碰撞过程的时间极短,且碰撞过程中没有机械能损失,要使物块
发生碰撞过程的时间极短,且碰撞过程中没有机械能损失,要使物块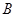 能够与挡板
能够与挡板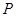 发生碰撞,初速度
发生碰撞,初速度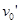 应满足的条件是什么?
应满足的条件是什么?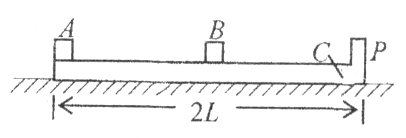
参考答案:(1)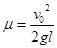 ,(2)
,(2)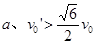 ,
,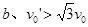
本题解析:(1)C被固定住,则A在摩擦力的作用下减速运动到B点,刚好碰到B的条件是达到B点A速度为零,即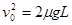 ,得
,得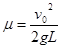
(2)a、要使物块A刚好与物块B发生碰撞,物块A运动到物块B处时,A、B的速度相等,
即v1=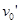 -μgt=
-μgt=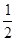 μgt?,得v1=
μgt?,得v1=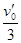 ?
?
设木板C在此过程中的位移为x1,则物块A的位移为x1+L,由动能定理?
-μmg(x1+L)=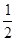 mv12-
mv12-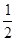 m
m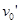 2
2
μmgx1=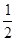 (2m)v12?
(2m)v12?
联立上述各式解得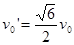 ,要使物块A、B发生相碰的条件是
,要使物块A、B发生相碰的条件是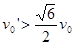
b、因为AB碰撞过程中没有机械能的损失,且两物块完全相同,所以碰撞时交换速度,就好像是A一直减速运动到挡板P一样,且刚好发生碰撞时,BC速度相等
即v2=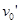 -μgt=
-μgt=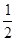 μgt?,得v2=
μgt?,得v2=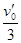
设木板C在此过程中的位移为x2,则物块AB的位移之和为x2+2L,由动能定理?
-μmg(x2+2L)=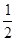 mv22-
mv22-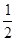 m
m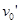 2
2
μmgx2=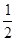 (2m)v22?
(2m)v22?
联立上述各式解得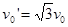 ,要使物块B与挡板发生相碰的条件是
,要使物块B与挡板发生相碰的条件是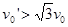
故答案为:(1)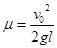 ,(2)
,(2)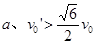 ,
,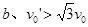
本题难度:简单
2、简答题 (1)有一群氢原子处于量子数n=4的激发态,已知氢原子的能级公式为En=
| E1 n2 |
参考答案:(1)一群处于n能级的氢原子向低能级跃迁,任意两个能级间产生一次跃迁,发出一种频率的光子,共产生x=n(n-1)2=4×32=6种频率不同的光子,
最大频率是n=4向n=1跃迁时发射的光子v=△Eh=E4-E1h=-15E116h
(2)①根据动量守恒定律得:mAvA=(mA+mB)v1
解得:v1=60m/s
②根据动量守恒定律得:mAvA=mAvA′+mBv2
解得:v2=50m/s
故答案为:(1)6;-15E116h? (2)①60m/s;②50m/s
本题解析:
本题难度:一般
3、简答题 如图1-6-8所示,甲车质量为2 kg,静止在光滑水平面上,上表面光滑,右端放一质量为1 kg的小物体.乙车质量为4 kg,以5 m/s的速度向左运动,与甲车相碰后甲车获得8 m/s 的速度,物体滑到乙车上.若乙车足够长,上表面与物体的动摩擦因数为0.2,则物体在乙车上滑行多长时间相对乙车静止?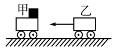
图1-6-8
参考答案:0.4 s
本题解析:甲、乙两车相撞过程中动量守恒,所以m乙v0=m甲v甲 + m乙v乙?①
小物体与乙车相互作用中动量守恒,设其最终速度为 v,则
m乙v乙=(m乙 + m物)v?②
设小物体在乙车上滑行时间为 t,则对小物体应用动量定理,得
μm物gt=m物v?③
代入数据联立①②③解得t="0.4" s.
本题难度:简单
4、简答题 (选修3-5)
(1)下列说法正确的是:
A、光电效应实验揭示了光的粒子性
B、某原子核经过一次α衰变后,核内质子数减少4个
C、重核的裂变过程质量增大,轻核的聚变过程有质量亏损
D、电子的衍射实验证实了物质波的假设是正确的
(2)如图所示,一对杂技演员(都视为质点)荡秋千时从A点(秋千绳OA处于水平位置)由静止出发绕悬点O下摆,当摆到最低点B时,男女演员在极短的时间内互相将对方沿水平方向推出,两人向相反方向做一平抛运动,并能安全落到地面.若女演员的落地点刚好在初始位置A点的正下方,且已知男演员质量是女演员质量的2倍,秋千的质量不计.秋千的绳长为R,O点距地面高度为5R,不计空气阻力.求男演员落地点C与O点的水平距离.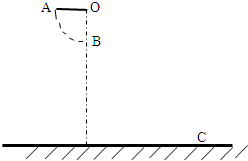
参考答案:(1)A、光电效应和康普顿效应深入的揭示了光的粒子性揭示了光的粒子性,A正确;
B、α衰变是原子核自发放射α粒子的核衰变过程.α粒子是电荷数为2、质量数为4的氦核He.质子数等于电荷数2,所以“核内质子数减少4个”是错误的;
C、重核的裂变过程和轻核的聚变过程都有质量亏损,所以C是错误的;
D、电子的衍射实验证实了物质的波动性,即物质波的假设是正确的;所以D是正确的;
故答案为AD.
(2)设分离前男女演员在秋千最低点B的速度为v0,由机械能守恒定律得:
(m1+m2)gR=12(m1+m2)v20 ①
设刚分离时男演员速度的大小为v1,方向与v0相同;女演员速度的大小为v2,方向与v0相反,由动量守恒,
(m1+m2)v0=m1v1-m2v2②
分离后,男演员做平抛运动,设男演员从被推出到落在C点所需的时间为t,
根据题给条件,由运动学规律,
4R=12gt2 ③
s=v1t④
根据题给条件,女演员的落地点刚好在初始位置A点的正下方,根据平抛有:
R=v2t ⑤
由以上各式可得:s=6.5R
答:男演员落地点C与O点的水平距离为6.5R.
本题解析:
本题难度:简单
5、简答题 湖面上静止的一条小船(如图所示)长l="3" m,质量M="120" kg.质量为m="60" kg的人从船头走到船尾,求此过程中人和船相对于地面的位移s1、s2.
参考答案:2 m? 1 m
本题解析:人和船组成的系统所受合外力为零,动量守恒,二者动量大小满足mv1-Mv2=0
因此,可以用各自的平均速度表示动量守恒m 1=M
1=M 2
2
而二者运动时间相同,各自相对于地面位移可表示为s1= 1t? s2=
1t? s2= 2t
2t
动量守恒可变形为m 1t=M
1t=M 2t,即ms1=Ms2?①
2t,即ms1=Ms2?①
可以用二者相对于地面的位移和质量的乘积表示动量关系,就是平均动量守恒.
整个运动过程中的位移可由右图表示,s1+s2="l?" ②
由方程①②可得
s1= =
= ?m="2" m? s2=
?m="2" m? s2= =
= ?m="1" m.
?m="1" m.
本题难度:简单