时间:2018-10-01 01:23:31
1、选择题 物体从静止不动的粗糙斜面上加速下滑的 过程,下列说法正确的是
过程,下列说法正确的是
A.重力和斜面对物体的支持力都做了正功
B.物体的机械能守恒
C.物体的机械能减少了
D.重力势能减少了,因为重力做了负功
参考答案:C
本题解析:略
本题难度:简单
2、选择题 如图,用细丝线悬挂的带有正电荷的小球,质量为m,处在水平向右的匀强电场中,在电场力作用下,小球在最低点由静止释放,经过b点后还可以再向右摆动,则在小球由a摆到b这一过程中,下列说法正确的是(?)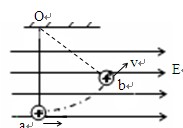
A.重力势能增大, 电势能减小,机械能增大
B.重力势能增大, 电势能减小, 机械能守恒
C.重力势能减小,电势能减小,机械能减小
D.重力势能增大, 电势能减小,机械能守恒
参考答案:A
本题解析:小球由最低点开始向右摆动,克服重力做功,其重力势能增大,电场力方向水平向右,电荷沿电场力方向发生了位移,电场力做正功,电势能减小,过程中电场力做功,所以机械能不守恒,电场力做正功,故物体的机械能增大,故选A,
点评:本题要抓住重力做功与重力势能变化的关系、电场力做功与电势能变化的关系判断.能量问题,首先要搞清几种形式的能,再根据功与能对应的关系分析.
本题难度:一般
3、计算题 (6分)如图所示,在光滑水平面上放置A、B两物体,质量均为m,其中B物体带有不计质量的弹簧静止在水平面内。A物体以速度v0向 右运动,并压缩弹簧。求:
右运动,并压缩弹簧。求:
(1)弹簧压缩量达到最大时A、B两物体的速度VA和VB。
(2)弹簧弹性势能的最大值EP。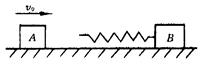
参考答案:(1)V0/2
(2)m V02/4
本题解析:略
本题难度:简单
4、计算题 (7分)风力发电是目前可再生能源中技术比较成熟,具有规模化开发条件和商业发展前景的发电技术。小型独立风力发电系统一般不并网发电,只能独立使用,单台装机容量通常不超过10KW。它的构成为:风力发电机+充电器+数字逆变器。风力发电机由机头、转体、尾翼、叶片组成。叶片用来接受风力并通过机头转为电能;尾翼使叶片始终对着来风的方向从而获得最大的风能;转体能使机头灵活地转动以实现尾翼调整方向的功能;机头的转子是永磁体,定子是绕组切割磁感线产生电能。因风量不稳定,故小型风力发电机输出的是13-25V变化的交流电,须经充电器整流再对蓄电池充电,使风力发电机的产生的电能变能化学能。最后经逆变处理后供给用户使用。某学习小组对一小型风力发电机进行测定风速实验:将一铜棒与风力发电系统的输出端构成回路(注:风力发电机与铜棒直接相连,连接导线末画出)如图所示。铜棒ab长为0.5m,质量0.2Kg,两端用轻铜线相连。整个装置处在竖直向上的匀强磁场中,磁感应强度B="2T." 当有风速4m/s吹向风叶,铜棒与竖直方向成37°角且偏向纸内的位置时,铜棒处于受力平衡状态。
(1)此时铜棒中通过的电流大小与方向。
(2)如风力发电机能把风能的30%转化为发电机的机械能,发电系统的效率为50%(其他能量损失一概不计),已知此小型风力发电系统输出电压恒定为24V,问当铜棒与竖直方向成53°角平衡时风速为多少m/s?(g取10m/s2,ρ空气=1.29Kg/m3,sin370=0.6,cos370="0.8" )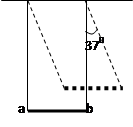
参考答案:(1)1.5A? b指向a?(2)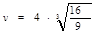
本题解析:(1)?根据左手定则:电流方向为? b指向a?(1分)
BIL=mgtanθ(1分)
I=mgtanθ/BL=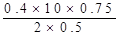 ="1.5" (A)?(1分)
="1.5" (A)?(1分)
(2)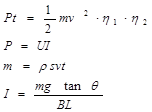
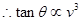 ?(3分)
?(3分)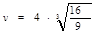 ?(1分)
?(1分)
本题难度:简单
5、选择题 如图所示,一个小球(视为质点)从H=12m高处,由静止开始通过光滑弧形轨道AB,进入半径R=4m的竖直圆环,圆环动摩擦因数处处相等,当小球沿BEC到达环顶C时,刚好对轨道压力为零;沿CFB圆弧滑下后,进入光滑弧形轨道BD,且到达高度为h的D点时的速度为零,则h值可能为(g=10m/s2,所有高度均相对B点而言) 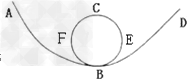
[? ]
A.11m?
B.10m?
C.8.5m?
D.7m?
参考答案:C
本题解析:
本题难度:一般