时间:2018-10-01 01:23:31
1、选择题 一个人把重物加速上举到某一高度，下列说法正确的是（ ）
A．物体所受的合外力对它所做的功等于物体机械能的增量
B．物体所受合外力对它所做的功等于物体的动能的增量
C．人对物体所做的功等于物体机械能的增量
D．物体克服重力所做的功等于物体的重力势能的增量
参考答案：A、根据动能定理物体所受的合外力对它所做的功等于动能的改变量，故A错误B正确；
C、重力以外的力做功等于机械能的改变量，即人对物体所做的功等于物体机械能的增量，C正确；
D、物体克服重力所做的功等于物体的重力势能的增量，D正确；
故选：BCD．
本题解析：
本题难度：简单
2、计算题 如图所示,质量为3 m的足够长木板C静止在光滑水平面上,质量均为m的两个小物体A?B放在C的左端,A?B间相距s0,现同时对A?B施加水平向右的瞬时冲量而使之分别获得初速度v0和2v0,若A?B与C之间的动摩擦因数分别为μ和2μ,则
(1)最终A?B?C的共同速度为多大?
(2)求运动过程中A的最小速度?
(3)A与B最终相距多远?
(4)整个过程中A?B与木板C因摩擦所产生的热量之比为多大?
参考答案：(1)0.6v0? (2)vAC=0.5v0? v0=vB
(3)
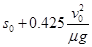?(4)5?27
本题解析：(1)由于A?B?C三个物体构成的系统在水平方向不受外力,所以由动量守恒定律可得
mv0+2mv0=5mv
最终A?B?C的共同速度为
v=0.6v0.
(2)设经t时间A与C恰好相对静止,此时A的速度最小,设为vAC,此时B的速度为vB,由动量守恒和动量定理得
mv0+2mv0=4mvAC+mvB
-μmgt=m(vAC-v0)
(μmg+2μmg)t=3mvAC
解得vAC=0.5v0? vB=v0.
(3)在A与C相对静止前,三个物体的加速度大小分别为aA=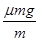
=μg? aB=
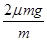=2μg? aC=
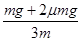=μg
A?B做匀减速运动,C做匀加速运动;在A与C相对静止后,三个物体的加速度大小又分别为
aA′=aC′=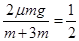
μg? aB′=aB=2μg
当A?C相对静止后,A?C做匀加速运动,B做匀减速运动,最终三个物体以共同速度匀速运动.在开始运动到三个物体均相对静止的过程中A?B相对于地面的位移分别为
sA=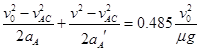
sB=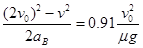
所以,A与B最终相距
Δs=s0+sB-sA=s0+0.425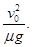
(4)设整个运动过程中A相对于C滑行距离为s,则B相对于C滑行的距离为s+Δs-s0,由动能定理得
μmgs+2μmg(s+Δs-s0)=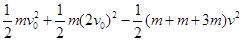
QA=μmgs
QB=2μmg(s
+Δs-s0)
解得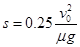
整个过程中A?B与木板C因摩擦所产生的热量之比为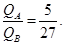
本题难度：一般
3、选择题 如图所示，竖立在水平地面上的轻弹簧下端固定．一铁块从它的正上方自由下落，从铁块开始接触弹簧到铁块第一次速度为零的过程中（ ）
A．弹簧的弹力对铁块先做正功后做负功
B．铁块的合外力先做正功后做负功
C．铁块动能最大时，弹簧的弹性势能最小
D．铁块的重力势能的减少量大于弹簧的弹性势能的增加量?
参考答案：A、铁块开始接触弹簧下降，重力大于向上的弹力，铁块加速向下运动，之后，重力小于弹力，合力向上，铁块向下减速运动，直到速度为零，铁块所受弹力始终向上，而运动方向向下，故弹力对铁块做负功，故A错误；
B、根据A的分析可知，合力先做正功后做负功，故B正确；
C、弹簧在被压缩到最长时即铁块速度为零时弹性势能最小，故C错误
D、从铁块开始接触弹簧到铁块第一次速度为零的过程中，重力和弹簧弹力做功，小球和弹簧系统机械能守恒，故小球重力势能的减小等于弹性势能的增加，故D错误．
故选：B
本题解析：
本题难度：一般
4、选择题 如图所示,斜面体B静置于水平桌面上．一质量为m的木块A从斜面底端开始以初速度v0沿斜面上滑，然后又返回出发点，此时速度为v，且v<v0．在上述过程中斜面体一直没有移动，由此可以得出：
A．A上滑过程桌面对B的支持力比下滑过程大
B．A上滑过程中桌面对B的静摩擦力比下滑过程大
C．A上滑时机械能的减小量等于克服重力做功和产生内能之和
D．A上滑过程与下滑过程，A、B系统损失的机械能相等
参考答案：ＢＤ.
本题解析：
考查受力分析、上滑对B的摩擦力方向沿斜面向上，下滑沿斜面向下，故A上滑过程桌面对B 的支持力比下滑过程小，A错误，上滑时的加速度大于下滑时的加速度，所以相当于对整体施加一个斜向下的力，所以上滑时施加的力大于下滑时时间的力，故根据力的分解可得A上滑过程中桌面对B的静摩擦力比下滑过程大，B正确；A上滑时机械能的减小量等于克服摩擦力产生的内能，C错误；A上滑过程与下滑过程，摩擦力大小相等、运动的路程相等，则做功相等，故系统损失的机械能相等，D正确。
点评：做本题的关键是理解上滑和下滑过程中小物体的加速度的关系
本题难度：一般
5、计算题 （18分）如图所示，劲度系数为k的轻质水平弹簧的左端固定在质量为mA=4m的物块A上，右端系一不可伸长的轻质细线，细线绕过轻质光滑的定滑轮后与质量为mB=2m的小物块B相连．物块A放在足够长的水平桌面上，它与桌面间的摩擦因数m，且知物块A与桌面的最大静摩擦力正好等于滑动摩擦力．滑轮以左的细线始终处于水平，整个系统当初处于静止状态．某时刻，一颗质量等于m的子弹以初速度v0水平击中物块A，并留在其中，物块A向前滑行一小段距离s而停下，此后将不再滑动．试求：
（1）子弹击中物块A后的瞬时，物块A的速度．
（2）物块A停下后，物块B加速度的最大值应为多少？
（3）物块A停下后，物块B的最大速度．
参考答案：见解析
本题解析：（1）可以认为子弹击中物块A的过程中，子弹与物块A的动量守恒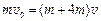
?①
可得子弹击中物块A后的瞬时，物块A的速度为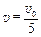
?②
（2）物块A停下后，要保证其不再滑动，弹簧的拉力至多等于物块A受到的最大静摩擦力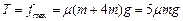
?③
因此可得物块B加速度的上限为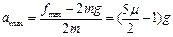
?④
（3）物块A停下后，物块B将做简谐运动，且当它处于平衡位置时，速度最大，而此时，弹簧的长度正好与初始时刻相同，即弹簧的弹性势能与初始时刻相等．由功能关系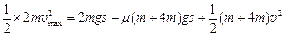
?⑤
可解得物块A停下后，物块B的最大速度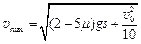
?⑥
本题难度：一般