时间:2018-10-01 01:10:55
1、选择题 如图所示,在真空中,匀强电场E的方向竖直向下,水平匀强磁场B垂直纸面向里,三个液滴a、b、c带有等量同种电荷。已知a静止,油滴b水平向右匀速运动,油滴c水平向左匀速运动。三者质量ma、mb和mc相比较 (?)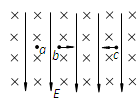
A.ma>mb>mc
B.mb>ma>mc
C.mc>ma>mb
D.ma=mb=mc
参考答案:C
本题解析:共点力作用下物体平衡专题.
分析:三个带电油滴都受力平衡,根据共点力平衡条件列式求解即可.
解:a球受力平衡,有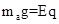 ?①
?①
重力和电场力等值、反向、共线,故电场力向上,由于电场强度向下,故球带负电;
b球受力平衡,有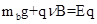 ?②
?②
c球受力平衡,有?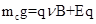 ?③
?③
解得mc>ma>mb
本题难度:简单
2、计算题 如图所示,两个界面S1和S2互相平行,间距为d,将空间分为三个区域。Ⅰ和Ⅲ两区域内有方向指向纸内的匀强磁场,磁感应强度分别为B1和B2。区域Ⅱ内是匀强电场E,方向从S1垂直指向S2。一质量为m、电量为-q的粒子(重力不计)以平行于电场线的初速度v0,从与S1相距为d/4的O点开始运动,为使该粒子沿图中的轨迹运动(轨迹的两个半圆的半径相等)。求:
(1)磁感应强度B1:B2之比应是多少?
(2)场强E应满足什么条件?
参考答案:(1)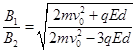 (2)
(2)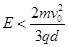
本题解析:(1)带电粒子在区域Ⅰ、Ⅲ两区中均做匀速圆周运动,粒子由洛伦兹力充当向心力,由牛顿第二定律得: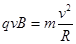 ,则
,则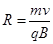
由题设可知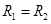 ,即
,即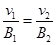
在电场中运动的过程中, 从O点到界面S1,由动能定理得: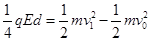
解得: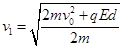
从界面S1到界面S2,由动能定理得: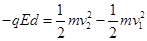 解得:
解得: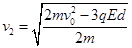
所以可得: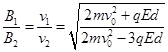
(2)为使该粒子沿图中的轨迹运动,粒子到达S2边界上的速度应有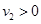 ,即
,即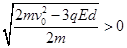
解得: 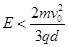
本题难度:一般
3、计算题 如图所示,光滑绝缘水平面的上方空间被竖直的分界面MN分隔成两部分,左侧空间存在一水平向右的匀强电场,场强大小?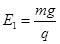 右侧空间有一长为R=0.8m的绝缘轻绳,绳的一端固定于O点,另一端拴一个质量m2=m的不带电的小球B在竖直平面内做顺时针方向的圆周运动,运动到最低点时速度大小vB=8m/s,小球B在最低点时与地面接触但没有弹力. 在MN左侧空间中有一个质量为m1=m的带正电的物体A,电荷量大小为q,在水平面上与MN界面水平间距为L处由静止释放,恰好与运动到最低点处的B发生正碰,并瞬间粘合成一个整体C,碰后瞬间在MN的右侧空间立即加上一竖直向上的匀强电场,场强大小E2=3E1(g=10m/s2)
右侧空间有一长为R=0.8m的绝缘轻绳,绳的一端固定于O点,另一端拴一个质量m2=m的不带电的小球B在竖直平面内做顺时针方向的圆周运动,运动到最低点时速度大小vB=8m/s,小球B在最低点时与地面接触但没有弹力. 在MN左侧空间中有一个质量为m1=m的带正电的物体A,电荷量大小为q,在水平面上与MN界面水平间距为L处由静止释放,恰好与运动到最低点处的B发生正碰,并瞬间粘合成一个整体C,碰后瞬间在MN的右侧空间立即加上一竖直向上的匀强电场,场强大小E2=3E1(g=10m/s2)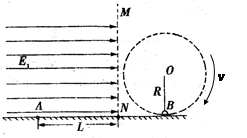
(1)如果L=0.2m,求出整体C运动到最高点时的瞬时速度大小,及此时绳的拉力是物体重力的多少倍?
(2)当L满足什么条件时,整体C可以在竖直面内做一个完整的圆周运动?
参考答案:(1)T="7.25" mg?(2)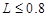 m或
m或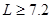 m,整体C在竖直面内做一个完整的圆周运动.
m,整体C在竖直面内做一个完整的圆周运动.
本题解析:(1)物A与B碰前速度为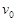 ,有动能定理:
,有动能定理: ?∴
?∴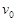 ="2" m/s
="2" m/s
A、B作用动量守恒:
∴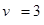 m/s,即C顺时针转动
m/s,即C顺时针转动
C有最底点→最高点速度为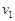 有动能定理:
有动能定理: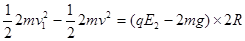
∴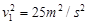 ?即
?即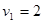 m/s?…………5分
m/s?…………5分
在最高点处: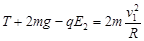 ∴T="7.25" mg?…………5分
∴T="7.25" mg?…………5分
(2)合成C后:∵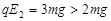 ,C的合力向上,
,C的合力向上,
即C在最底处有最小速度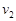 :
: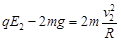 ∴
∴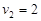 m/s
m/s
令C顺时针: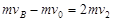 ,∴
,∴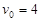 m/s,则
m/s,则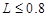 m?…………5分
m?…………5分
令C逆时针: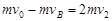 ,∴
,∴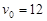 m/s,则
m/s,则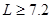 m?…………5分
m?…………5分
即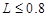 m或
m或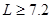 m,整体C在竖直面内做一个完整的圆周运动.
m,整体C在竖直面内做一个完整的圆周运动.
本题难度:一般
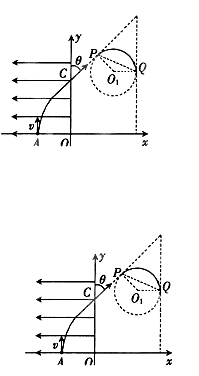
4、计算题 如图所示,在平面直角坐标系xOy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向里的有界圆形匀强磁场区域(图中未画出);在第二象限内存在沿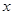 轴负方向的匀强电场.一粒子源固定在x轴上的A点,A点坐标为(-
轴负方向的匀强电场.一粒子源固定在x轴上的A点,A点坐标为(-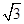 L,0)。.粒子源沿y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0,2L),电子经过磁场偏转后方向恰好垂直于x轴射入第四象限.(电子的质量间的相互作用.)求:
L,0)。.粒子源沿y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0,2L),电子经过磁场偏转后方向恰好垂直于x轴射入第四象限.(电子的质量间的相互作用.)求:
(1)第二象限内电场强度E的大小;
(2)电子离开电场时的速度方向与y轴正方向的夹角θ;
(3)圆形磁场的最小半径Rmin. 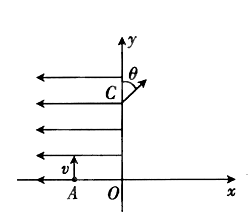
参考答案:(1)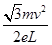 (2)θ=60°(3)Rmin=
(2)θ=60°(3)Rmin=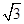 mv/eB
mv/eB
本题解析::解题指导:对于带电粒子在匀强电场中的运动运用类平抛运动规律解答。带电粒子进入匀强磁场中,洛伦兹力提供向心力,结合相关知识列方程解答。
解:(1)从A到C的过程中,电子做类平抛运动,有,
电子的加速度a=eE/m,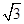 L =at2/2
L =at2/2
2L=vt,
联立解得E=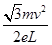 。
。
(2)设电子到达C点的速度大小为vC,方向与y轴正方向的夹角为θ。由动能定理,有: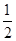 mvC2-
mvC2-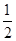 mv2=
mv2=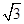 eEL
eEL
解得vC=2v。
cosθ=v/vC=0.5,
电子离开电场时的速度方向与y轴正方向的夹角θ=60°。
(3)电子运动轨迹如图所示。由公式qvCB=m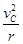 ,
,
解得电子在匀强磁场中做匀速圆周运动的半径r=2mv/eB。
电子在磁场中偏转120°后垂直于x轴射出,由三角形知识得磁场最小半径:
Rmin=PQ/2=rsinθ=rsin60°,
联立解得:Rmin=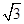 mv/eB。
mv/eB。
点评:此题考查带电粒子在电场中的类平抛运动和在匀强磁场中的匀速圆周运动。
本题难度:一般
5、计算题 如图所示为一速度选择器,也称为滤速器的原理图。K为电子枪,由枪中沿KA方向射出的电子,速率大小不一。当电子通过方向互相垂直的均匀电场和磁场后,只有一定速率的电子能沿直线前进,并通过小孔S。设产生匀强电场的平行板间的电压为300 V,间距为5 cm,垂直纸面的匀强磁场的磁感应强度为0.06 T,问:
(1)磁场的指向应该向里还是向外?
(2)速度为多大的电子才能通过小孔S? 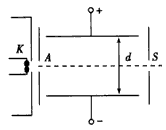
参考答案:解:(1)由题图可知,平行板产生的电场强度E方向向下,带负电的电子受到的电场力FE=eE,方向向上。若没有磁场,电子束将向上偏转,为了使电子能够穿过小孔S,所加的磁场施于电子束的洛伦兹力必须是向下的。根据左手定则分析得出,B的方向垂直于纸面向里
(2)电子受到的洛伦兹力为:FB=evB,它的大小与电子速率v有关,只有那些速率的大小刚好使得洛伦兹力与电场力相平衡的电子,才可沿直线KA通过小孔S
据题意,能够通过小孔的电子,其速率满足下式:evB=eE,解得:v=
又因为 ,所以
,所以
将U=300 V,B=0.06 T,d=0.05 m代入上式,得v=105m/s,即只有速率为105 m/s的电子可以通过小孔S
本题解析:
本题难度:困难