时间:2018-10-01 00:58:39
1、选择题 关于机械能守恒，下列叙述中正确的是
[? ]
A．作匀速直线运动物体的机械能一定守恒
B．作匀变速运动物体的机械能可能守恒
C．外力对物体做功为零时，机械能一定守恒
D．只有重力对物体做功，物体的机械能一定守恒
参考答案：BD
本题解析：
本题难度：简单
2、简答题 如图所示，一轻绳穿过光的定滑轮，两端各拴一小物块，它们的质量分别为m1、m2，已知m2=3m1，起始时m1放在地上，m2离地面高度为h=1.00m，绳子处于拉直状态，然后放手，设物块与地面相碰时完全没有弹起（地面为水平沙地），绳不可伸长，绳中各处拉力均相同，在突然提拉物块时绳的速度与物块相同，试求m2所走的全部路程（取三位有效数字）．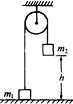
参考答案：1.13m
本题解析：m2从h高处下落，落地前的速度为v，对系统，由机械能守恒定律可得
? ①
m2落地与地面碰撞后，速度变为零，m1以速度v做竖直上抛运动，后又自由落下，在绳刚伸直但尚未绷紧时，其速度仍为v，在绳绷紧的瞬间m1的动量由m1v变为m1v1，m2的动量由0变为m2v1，因绳绷紧的瞬间，绳中拉力远大于物块重力，因此可以认为这一过程动量守恒，选m1、m2的运动方向为正方向，有
m1v=(m1＋m2)v1，? ②
这以后m2以速度v1向上运动，m1以v1向下运动，当m2上升至最高点(设其高度为h1)时，m1、m2的速度皆为零，由机械能守恒有
? ③
由①②③式解得 
? ④
m2到达高度h1后，又从该处下落，并到达地面，与前面的过程相似，m2第二次上升到最点，其高度为h2，按上面的计算，有
依次类推，可得
因而m2走过的路程为
.
本题难度：一般
3、选择题 如图所示，在倾角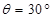
的光滑固定斜面上，放有质量分别为1kg和2kg的小球A和B，且两球之间用一根长L=0.3m的轻杆相连，小球B距水平面的高度h=0.3m．现让两球从静止开始自由下滑，最后都进入到上方开有细槽的光滑圆管中，不计球与圆管内壁碰撞时的机械能损失，g取10m/s2．则下列说法中正确的有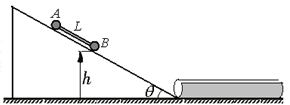
A．从开始下滑到A进入圆管整个过程，小球A与地球两者组成的系统机械能守恒
B．在B球未进入水平圆管前，小球A与地球组成系统机械能守恒
C．两球最后在光滑圆管中运动的速度大小为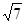
m/s
D．从开始下滑到A进入圆管整个过程，轻杆对B球做功1J
参考答案：BCD
本题解析：B球未进入水平圆管前A、B都只受重力做功，A、B机械能守恒定律，B进入圆管的过程中，A机械能减小，B机械能增加，A错误、B正确；A、B整体机械能守恒，全部进入圆管中，速度为m/s，C正确；B的机械能增加1J，D正确。
考点：机械能守恒定律
本题难度：一般
4、计算题 如图所示，一很长的、不可伸长的柔软轻绳跨过光滑定滑轮，绳两端各系一小球
a和b。a球质量为2m，静置于地面；b球质量为3m，用手托住，高度为h，此时轻绳刚好拉紧．从静止开始释放b后，求a可达到的最大高度.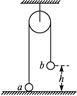
参考答案：1.2h
本题解析：在b球落地前，a．b球组成的系统机械能守恒，且a．b两球速度大小相等，设为v，根据机械能守恒定律有：3mgh－2mgh＝
?(2m＋3m)v2，
解得：
b球落地时，a球高度为h，之后a球向上做竖直上抛运动，由机械能守恒有，?(2m)v2＝2mgΔh
Δh＝＝0.2h
所以a球可能达到的最大高度为H=h+0.2h=1.2h．
点评：在a球上升的全过程中，a球的机械能是不守恒的，所以在本题中要分过程来求解，第一个过程系统的机械能守恒，在第二个过程中只有a球的机械能守恒．
本题难度：一般
5、选择题 物体在下列运动过程中，机械能守恒的是
A．直升机载物匀速上升
B．起重机匀速下放物体
C．物体沿光滑斜面加速下滑
D．电梯载物匀加速上升
参考答案：C
本题解析：直升机匀速上升，动能不变，势能增加，故机械能不守恒，A错误
起重机匀速下降，动能不变，势能减小，机械能不守恒，B错误
沿光滑斜面下滑，过程中只有重力做功，机械能守恒，C正确
电梯匀加速上升过程中，牵引力做正功，机械能不守恒，D错误
故选C
点评：在判断机械能守恒时，一可以判断动能与势能之和是否恒定，二可以判断是否存在重力以外的力做功
本题难度：简单