时间:2018-03-18 10:03:59
1、简答题 某一核反应的模型中质量为m0、速度为v0的粒子与一个质量为M、静止的原子核碰撞后合为一体，又迅速发生变化放出质量为m、速度为v的另一个粒子，此粒子的速度v与v0反方向.试问余下的反冲核的反冲速度为多大?
参考答案：
本题解析：由动量守恒定律得m0v0=(M+m0-m)v′-mv
余下的反冲核的反冲速度为v′=.
本题难度：简单
2、选择题 质量为M的快艇携带一颗质量为m的鱼雷，两者一起以速度v向前运动．快艇沿前进方向发射鱼雷后，速度减为原来的
| 1 3 |
| 2M+3m 3m |
| 2M 3m |
| 4M-m 3m |
| 4M 3m |
参考答案：不计水的阻力，快艇和鱼雷组成的系统在发射的瞬间动量守恒，取快艇原来速度方向为正方向，根据动量守恒定律有：
Mv=（M-m）?13v+mv′．
解得鱼雷的发射速度为：v′=2M+3m3mv．故A正确，B、C、D错误．
故选：A．
本题解析：
本题难度：一般
3、简答题 如图5－13所示，在光滑水平轨道上有一小车质量为M2，它下面用长为L的绳系一质量为M1的砂袋，今有一水平射来的质量为m的子弹，它射入砂袋后并不穿出，而与砂袋一起摆过一角度θ。不计悬线质量，试求子弹射入砂袋时的速度V0多大？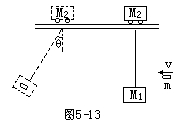
参考答案：从子弹入射前到摆动至最同点具有共同速度v为止，在这个过程中，水平方向不受外力，所以、动量守恒，由动量守恒定律有：
mv0=(M1+M1+m)v ③
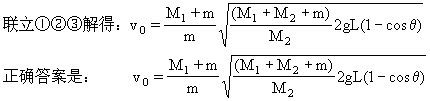
本题解析：【错解分析】错解： 由动量守恒定律：mv0=(M1＋M2+m)v
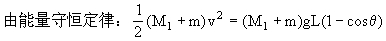
解得：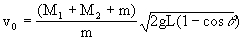
没有很好地分析物理过程，盲目模仿，没有建立正确的物理模型，简单地将此类问题看成“冲击摆”，缺少物理模型变异的透彻分析。事实上，此题与“冲击摆”的区别在于悬点的不固定，而是随着小车往前移动的。当摆摆到最高点时，(M1＋m)只是竖直方向的速度为零，而水平方向依然具有一定速度，即在最高点处(M1＋m)具有动能。这一点是不少学生在分析物理过程及建立物理模型时最容易产生的错误。
【正确解答】 子弹射入砂袋前后动量守恒，设子弹打入砂袋瞬间具有速度v0′，由动量守恒定律：
mv0=(M1＋m)v′ ①
此后(M1＋m)在摆动过程中，水平方向做减速运动，而M2在水平方向做加速运动，当(M1+m)与M2具有共同水平速度时，悬线偏角θ达到最大，即竖直向上的速度为零，在这一过程中。满足机械能守恒，设共同速度为v，由机械能守恒有：
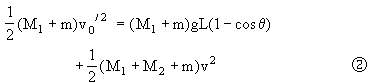
但式①，②中有三个未知量，v0，v0′，v，还需再寻找关系。
从子弹入射前到摆动至最同点具有共同速度v为止，在这个过程中，水平方向不受外力，所以、动量守恒，由动量守恒定律有：
mv0=(M1+M1+m)v ③
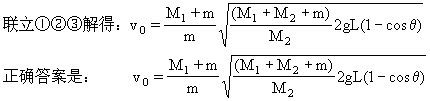
【小结】 对于大部分学生来讲，掌握一定的物理模型并不困难，困难在于题目变化，新的题目中的模型如何能够转换成为我们熟悉的，旧有的，规范的物理模型中，进而用比较普遍运用的物理规律去求解，此题就是从滑动的小车摆(暂且这样称呼)迁延至“冲击摆”，找出两者之间的共同点与区别，达到解决问题的目的。
本题难度：简单
4、选择题 （5分）、如下图所示，质量为M的盒子放在光滑的水平面上，盒子内表面不光滑，盒内放有一块质量为m的物体．从某一时刻起给m一个水平向右的初速度v0，那么在物块与盒子前后壁多次往复碰撞后（?）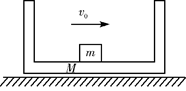
A．两者的速度均为零
B．两者的速度总不会相等
C．车的最终速度为mv0/M，向右
D．车的最终速度为mv0/（M＋m），向右
参考答案：D
本题解析：根据动量守恒，物块与盒子前后壁多次往复碰撞，最后以相同的速度向右运动，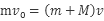
?所以：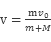
?，选项D正确。
本题难度：一般
5、实验题 如图所示，在实验室用两端带竖直挡板C、D的气垫导轨和有固定挡板的质量都是M的滑块A、B，做探究碰撞中不变量的实验： 
①把两滑块A和B紧贴在一起，在A上放质量为m的砝码，置于导轨上，用电动卡销卡住A和B，在与A和B的固定挡板间放一弹簧，使弹簧处于水平方向上的压缩状态。
②按下电钮使电动卡销放开，同时启动两个记录两滑块运动时间的电子计时器，当A和B与挡板C和D碰撞同时，电子计时器自动停表，记下A至C运动时间t1，B至D运动时间t2。
③重复几次取t1、t2的平均值。
请回答以下几个问题：
（1）在调整气垫导轨时应注意_________；
（2）应测量的数据还有_________；
（3）作用前A、B两滑块速度与质量乘积之和为_________，作用后A、B两滑块速度与质量乘积之和为_________。
参考答案：（1）用水平仪测量使得导轨水平
（2）A至C的距离L1、B至D的距离L2
（3）0，
本题解析：
本题难度：一般