时间:2018-03-18 09:35:22
1、选择题 水平转动的圆盘上有质量相同的A、B两个物体，A、B到转动中心O 的距离分别为R、2R，A、B两个物体通过一根不可伸长的轻绳相连，且绳子刚好伸直。（A、B两个物体可以看成质点，最大静摩擦力等于滑动摩擦力）在圆盘的转速从0开始逐渐增大到最终A、B相对于圆盘出现滑动的过程中，下列说法正确的是（?）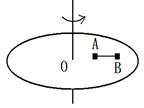
A. A物体所受到的摩擦力逐渐增大
B. B物体所受到的摩擦力逐渐增大
C. 绳子上的拉力逐渐增大
D. 如果 A、B没有绳子相连，在转速增大过程中，B首先相对滑动
参考答案：AD
本题解析：水平转动的圆盘上的两物体，角速度相等，根据向心力公式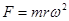
，半径越大，需要的向心力越大，所B先达到最大静摩擦力，然后通过绳子对A物体有拉力作用，此后B摩擦力保持不变，而A的摩擦力先逐渐减小，后反方向逐渐变大，直到最终A、B相对于圆盘出现滑动，从以上可以得出，如果A、B没有绳子相连，当转速增大到一定程度，则B首先相对滑动，AD正确。
本题难度：简单
2、简答题 某同学设想用带电粒子的运动轨迹做出“0”字样，首先，在真空空间的竖直平面内建立xoy坐标系，在x1=-0.1m和x2=0.1m处有两个与y轴平行的竖直界面PQ、MN把空间分成Ⅲ、Ⅱ、Ⅰ三个区域，在这三个区域中分别存在匀强磁场B3、B2、B1，其大小满足B2=2B3=2B1=0.02T，方向如图所示．在Ⅱ区域中的x轴上、下两侧还分别存在匀强电场E1、E2（图中未画出），忽略所有电、磁场的边缘效应，ABCD是以坐标原点O为中心对称的正方形，其边长a=0.2m．现在界面MN上的A点沿x轴正方向发射一个比荷q/m=1.0×108C/kg的带正电的粒子（其重力不计），粒子恰能沿图中实线运动，途经B、C、D三点后回到A点，做周期性运动，轨迹构成一个“0”字，已知粒子每次穿越Ⅱ区域时均作直线运动．试求：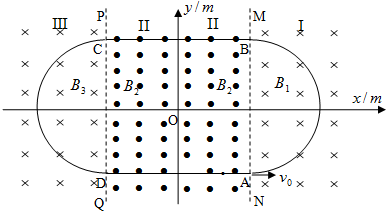
（1）粒子自A点射出时的速度大小v0；
（2）电场强度E1、E2的大小和方向；
（3）粒子作一次周期性运动所需的时间．
参考答案：（1）带电粒子在区域Ⅰ中做匀速圆周运动，直径2R=a，由
? qv0B1=mv20R
得v0=qB1Rm=1×105m/s
（2）带电粒子在区域Ⅱ中做匀速直线运动，电场力与洛伦兹力平衡，由左手定则判断可知洛伦兹力的方向沿y轴正方向，则电场力沿y负方向，电场强度E1也沿y轴负方向．
? 且有? qv0B2=qE1，则得E1=v0B2=2×103N/C．
同理，E2=v0B2=2×103N/C，方向沿y轴正方向．
（3）粒子在区域Ⅱ运动的时间t1=2×av0
在区域Ⅰ和Ⅲ中运动的时间t2=T=2πmqB1
则得粒子作一次周期性运动所需的时间t=t1+t2=2×av0+2πmqB1
代入数据解得，t=（4+2π）×10-6s
答：
（1）粒子自A点射出时的速度大小v0是1×105m/s．
（2）电场强度E1的大小为2×103N/C，方向沿y轴负方向；E2的大小为2×103N/C，方向沿y轴正方向．
（3）粒子作一次周期性运动所需的时间是（4+2π）×10-6s．
本题解析：
本题难度：一般
3、简答题 如图所示，电源电动势E=60V，内阻r=1Ω，R1=3Ω，R2=6Ω．间距d=0.03m的两平行金属板A、B水平放置，闭合开关S，两板之间存在着匀强电场．在B板上开有两个间距为L=1.2m的小孔．M、N为两块同心1/4圆弧形金属板，圆心都在贴近B板的O′处，两板间的距离很近，两板上端的中心线正对着B板上的小孔（与B板的间隙可忽略不计），下端切线水平，P点恰好在O′的正下方，两圆弧形金属板间的电场强度可认为大小处处相等，方向都指向O′．现从正对B板小孔紧靠A板的O处由静止释放一个质量为m=1.0×10-5Kg、电量为q=1×10-3C的带正电微粒（微粒的重力不计），问：
（1）微粒穿过B板小孔时的速度多大；
（2）为了使微粒能在MN板间运动而不碰板，MN板间的电场强度大小应满足什么条件；
（3）从释放微粒开始，经过多长时间微粒通过两圆弧形金属板？
（4）为了让P点出射的带电粒子能射到B板的右侧C点小孔，现在P点外侧虚线框内另加一个竖直方向的有界匀强电场，则电场强度E为多少？
参考答案：（1）因为平行金属板和电阻R1并联，故根据闭合电路欧姆定律可得：
UAB=R1R1+R2+rE=33+6+160V=18V
根据动能定理，粒子通过AB过程中电场力对粒子做的功等于粒子动能的变化：
qUAB=12mv2-0
得粒子获得的速度v=
本题解析：
本题难度：一般
4、选择题 一个质量为M的物体在水平转盘上，距离转轴的距离为r，当转盘的转速为n时，物体相对于转盘静止，如果转盘的转速增大时，物体仍然相对于转盘静止，则下列说法中正确的是
[? ]
A．物体受到的弹力增大
B．物体受到的静摩擦力增大
C．物体受到的合外力不变
D．物体对转盘的压力减小
参考答案：B
本题解析：
本题难度：一般
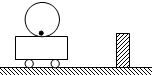
5、选择题 半径为R的圆桶固定在小车上，有一光滑的小球静止在圆桶的最低点，小车以速度v向右匀速运动，当小车遇到一个障碍物突然停止运动时，小球在圆桶内升高的高度可能为（ ）
A．等于
| v2 2g |
| v2 2g |
| v2 2g |
参考答案：小球小球由于惯性会继续运动，可能会越过最高点做圆周运动，也有可能达不到四分之一圆周，速度减为零，也有可能越过四分之一圆周但越不过圆桶的最高点．
1、若越过最高点做圆周运动，则在圆桶中上升的高度等于2R．
2、若达不到四分之一圆周，速度减为零，根据机械能守恒，12mv2=mgh，h=v22g．
3、若越过四分之一圆周但越不过圆桶的最高点，则会离开轨道做斜抛，在最高点有水平速度，根据机械能守恒得，12mv2=mgh+12mv′2，上升的高度小于v22g．故A、C、D正确，B错误．
故选ACD．
本题解析：
本题难度：简单