时间:2017-11-10 08:16:32
1、实验题 某同学在做探究弹力和弹簧伸长的关系的实验中，设计了图1所示的实验装置．他先测出不挂钩码时弹簧的自然长度，再将钩码逐个挂在弹簧的下端，每次都测出相应的弹簧总长度，将数据填在下面的表中．(弹簧始终在弹性限度内)
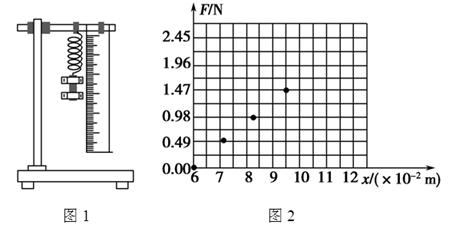
(1)根据实验数据在图2的坐标纸上已描出了前四次测量的弹簧所受弹力大小F跟弹簧总长x之间的函数关系点，请把第5、6次测量的数据对应的点描出来，并作出F-x图线．
(2)图线跟x坐标轴交点的物理意义是__________________________________．
(3)该弹簧的劲度系数k＝________.(结果保留两位有效数字)
参考答案：（1）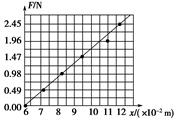
(2)弹簧的原长(3)42 N/m
本题解析：（1）根据实验数据在坐标纸上描出的点，基本上在同一条直线上．可以判定F和L间是一次函数关系．画一条直线，使尽可能多的点落在这条直线上，不在直线上的点均匀地分布在直线两侧，如右图：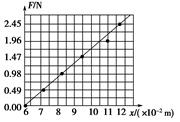
（2）图线与坐标轴交点即表示弹簧所受弹力大小F=0时，弹簧的长度． 所以其物理意义：表示弹簧的 原长
（3）根据胡克定律得：由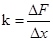
可得
．
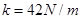本题难度：一般
2、选择题 如图所示，四根相同的弹簧都处于水平位置，右端都受到大小皆为F的拉力作用，而左端的情况各不相同：
①中的弹簧左端固定在墙上；
②中的弹簧左端受大小也为F的拉力作用；
③中的弹簧左端栓一个小物块，物块在光滑桌面上滑动；
④中的弹簧左端栓一个小物块，物块在有摩擦的桌面上滑动．
若认为弹簧的质量都为零，以l1、l2、l3、l4依此表示四根弹簧的伸长量，则有（ ）
A．l1＜l2
B．l2=l4
C．l3＜l1
D．l4＞l3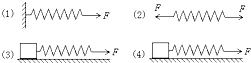
参考答案：弹簧受到的拉力与其伸长量（弹簧实际长度与原长之间的差值）成正比；由于右端受到大小皆为F，与左端的受力情况无关；故四根弹簧的伸长量都相同，即l1=l2=l3=l4；
故选：B
本题解析：
本题难度：简单
3、计算题 如图所示，一个重为G的小球套在竖直放置的半径为R的光滑大圆球上，一个劲度系数为k，原长为L（L<R）的轻弹簧，一端固定在大圆环顶点A，另一端与小球相连小球在大圆环上无可摩擦滑动，求：当环静止于B点时，弹簧有多长？
参考答案：
本题解析：设弹簧现长为
由几何知识可知：
（3分）
又
（2分）
（1分）
本题难度：简单
4、计算题 （15分）如图所示，在竖直方向上A、B物体通过劲度系数为k的轻质弹簧相连，A放在水平地面上，B、C两物体通过细绳绕过光滑轻质定滑轮相连，C放在固定的光滑斜面上，斜面倾角为30°，用手按住C，使细绳刚刚拉直但无拉力作用，并保证ab段的细绳竖直、cd段的细绳与斜面平行。已知A、B的质量分别为m1、m2，C的质量为2m，重力加速度为g，细绳与滑轮之间的摩擦力不计，开始时整个系统处于静止状态，释放C后它沿斜面下滑，斜面足够长，且物体A恰不离开地面。求：
(1)物体A恰不离开地面时，物体C下降的高度；
(2)其他条件不变，若把物体C换为质量为2（m+△m）的物体D，释放D后它沿斜面下滑，当A恰不离开地面时，物体B的速度为多大？
参考答案：（1）
（2）
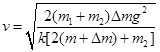
本题解析：(1)初始整个系统处于静止状态，以物体B为研究对象可知，弹簧处于压缩状态，则：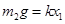
?（2分）
当物体A恰不离开地面时，以物体A为研究对象可知，弹簧处于伸长状态，则：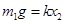
?（2分）
因而物体C下降的高度为：?
?（1分）
联立解得：?（2分）
（2）物体C沿斜面下滑，当物体A恰不离开地面时，物体C的速度为零，以物体C、B和弹簧整体为研究对象，根据机械能守恒定律可知：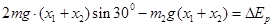
?（3分）
把物体C换为物体D后，当物体A恰不离开地面时，此时物体D和物体B的速度大小相等，以物体D、B和弹簧整体为研究对象，根据机械能守恒定律可知：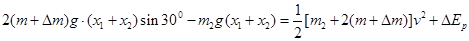
（3分）
联立解得物体B的速度大小为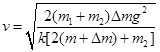?（2分）
本题难度：一般
5、实验题 某同学用单摆测重力加速度，
①他组装单摆时，在摆线上端的悬点处，用一块开有狭缝的橡皮夹牢摆线，再用铁架台的铁夹将橡皮夹紧，如图所示，这样做的目的是_______（填字母代号）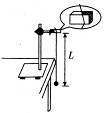
A.保证摆动过程中摆长不变
B.可使周期测量得更加准确
C.需要改变摆长时便于调节
D.保证摆球在同一竖直平面内摆动
②他组装好单摆后在摆球自然悬垂的情况下，用毫米刻度尺从悬点量到摆球的最低端的长度L=_________m，再用游标卡尺测量摆球直径D=________m，再测定了40次全振动的时间t=_________s，则单摆摆长l=_________m，重力加速度g=__________m/s2。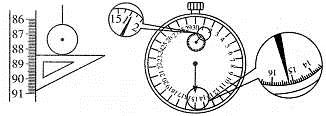
?
③如果测得的g值偏小，可能的原因是_______（填写代号）。
A.测摆长时，忘记了摆球的半径
B.摆线上端悬点未固定，振动中出现松动，使摆线长度增加了
C.开始计时时，秒表过早按下
D.实验中误将39次全振动次数记为40次
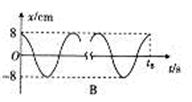
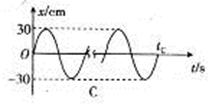
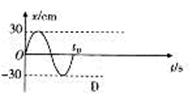
④下列振动图象真实地描述了对摆长约为1 m的单摆进行周期测量的四种操作过程，图中横坐标原点表示计时开始，A、B、C均为30次全振动的图象，已知sin5°=0.087，sin15°=0.26，这四种操作过程合乎实验要求且误差最小的是________（填字母代号）。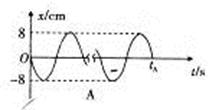
参考答案：①AC?②0.8840，0.0120，75.2，0.8780，9.78～9.82。?③BC?④A
本题解析：①那样做的目的就是为了便于调节摆长，把摆线夹得更紧一些，使摆动过程中摆长不变。因此A、C正确。
②刻度尺的读数是0.8840 m；游标卡尺的读数是0.0120 m；四十次全振动的时间为75.2 s；则单摆的摆长为
="0.8780" m；重力加速度根据单摆的周期公式有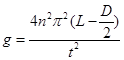
，代入数据解得g，在9.78～9.82 m/s2范围均算正确。
③测摆长时，忘记了摆球的半径，导致g偏大，选项A错误。摆线上端悬点未固定，振动中出现松动，使摆线长度增加了，导致周期变大，g值变小，选项B正确。开始计时时，秒表过早按下，导致时间t增大，g值变小，选项C正确。n变大，g变大，选项D错误。
④A、B的振幅为8 cm，它与摆长1 m的比值为0.08<sin5°，即摆角小于5°，而C、D的振幅为30 cm，它与摆长1 m的比值为0.30≈sin15°，即摆角大约为15°，单摆的周期公式只在摆角小于5°的条件下成立，选项C、D均错误。而实验在平衡位置开始计时测量时间的误差较小，选项A正确、B错误。
本题难度：简单